About Contact Pairs in Abaqus/Standard

Defining Contact Pairs

To define a contact pair, you must indicate which pairs of surfaces may interact with one another or which surfaces may interact with themselves. Contact surfaces should extend far enough to include all regions that may come into contact during an analysis; however, including additional surface nodes and faces that never experience contact may result in significant extra computational cost (for example, extending a secondary surface such that it includes many nodes that remain separated from the main surface throughout an analysis can significantly increase memory usage unless penalty contact enforcement is used).

Every contact pair is assigned a contact formulation (either explicitly or by default) and must refer to an interaction property. Discussion of the various available contact formulations (based on whether the tracking approach assumes finite- or small-sliding—and whether the contact discretization is based on a node-to-surface or surface-to-surface approach) is provided in Contact Formulations in Abaqus/Standard. Interaction property definitions are discussed in Assigning Contact Properties for Contact Pairs in Abaqus/Standard.

Defining Contact between Two Separate Surfaces

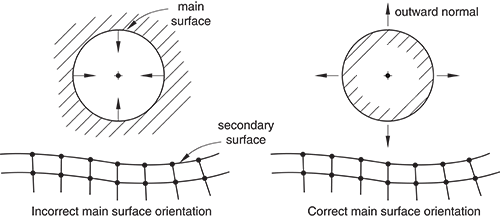
When a contact pair contains two surfaces, the two surfaces are not allowed to include any of the same nodes and you must choose which surface will be the secondary and which will be the main. The selection of main and secondary surfaces is discussed in detail in Choosing the Main and Secondary Surface Roles in a Two-Surface Contact Pair. For simple contact pairs consisting of two deformable surfaces, the following basic guidelines can be used:

The larger of the two surfaces should act as the main surface.
If the surfaces are of comparable size, the surface on the stiffer body should act as the main surface.
If the surfaces are of comparable size and stiffness, the surface with the coarser mesh should act as the main surface.

The finite-sliding, node-to-surface formulation is used by default (except in Abaqus/CAE, where the default is the finite-sliding, surface-to-surface formulation).

Defining Contact Pairs Using the Finite-Sliding, Node-to-Surface Formulation

A finite-sliding, node-to-surface formulation is available.

Input File Usage

CONTACT PAIR, INTERACTION=interaction_property_name
secondary_surface_name, main_surface_name

You can also specify the contact discretization directly:

CONTACT PAIR, INTERACTION=interaction_property_name, 
TYPE=NODE TO SURFACE
secondary_surface_name, main_surface_name

Abaqus/CAE Usage

Interaction module: Create Interaction: Surface-to-surface contact (Standard): select the main surface, click Surface or Node Region, select the secondary surface, 
Interaction editor, Sliding formulation: Finite sliding, Discretization method: Node to surface, Contact interaction property: interaction_property_name

Defining Contact Pairs Using the Finite-Sliding, Surface-to-Surface Formulation

A node-based secondary surface precludes the use of surface-to-surface discretization. Some contact capabilities are not available with the finite-sliding, surface-to-surface formulation, including crack propagation (see Crack Propagation Analysis).

Input File Usage

Use the following option to define contact constraints using the finite-sliding, surface-to-surface formulation:

CONTACT PAIR, INTERACTION=interaction_property_name, 
TYPE=SURFACE TO SURFACE
secondary_surface_name, main_surface_name

Abaqus/CAE Usage

Interaction module: Create Interaction: Surface-to-surface contact (Standard): select the main surface, click Surface, select the secondary surface, 
Interaction editor, Sliding formulation: Finite sliding, Discretization method: Surface to surface, Contact interaction property: interaction_property_name

Defining Contact Pairs Using the Small-Sliding, Node-to-Surface Formulation

The small-sliding tracking approach uses node-to-surface discretization by default. For an explanation of when the small-sliding tracking approach is appropriate in an analysis, see Using the Small-Sliding Tracking Approach.

Input File Usage

CONTACT PAIR, INTERACTION=interaction_property_name, 
SMALL SLIDING
secondary_surface_name, main_surface_name

You can also specify the contact discretization directly:

CONTACT PAIR, INTERACTION=interaction_property_name, 
SMALL SLIDING, TYPE=NODE TO SURFACE 
secondary_surface_name, main_surface_name

Abaqus/CAE Usage

Interaction module: Create Interaction: Surface-to-surface contact (Standard): select the main surface, click Surface or Node Region, select the secondary surface, 
Interaction editor, Sliding formulation: Small sliding, Discretization method: Node to surface, Contact interaction property: interaction_property_name

Defining Contact Pairs Using the Small-Sliding, Surface-to-Surface Formulation

A node-based secondary surface precludes the use of surface-to-surface discretization.

Input File Usage

CONTACT PAIR, INTERACTION=interaction_property_name, 
SMALL SLIDING, TYPE=SURFACE TO SURFACE 
secondary_surface_name, main_surface_name

Abaqus/CAE Usage

Interaction module: Create Interaction: Surface-to-surface contact (Standard): select the main surface, click Surface, select the secondary surface, 
Interaction editor, Sliding formulation: Small sliding, Discretization method: Surface to surface, Contact interaction property: interaction_property_name

Using Symmetric Main-Secondary Contact Pairs to Improve Contact Modeling

For node-to-surface contact it is possible for main surface nodes to penetrate the secondary surface without resistance with the strict main-secondary algorithm used by Abaqus/Standard. This penetration tends to occur if the main surface is more refined than the secondary surface or a large contact pressure develops between soft bodies. Refining the secondary surface mesh often minimizes the penetration of the main surface nodes. If the refinement technique does not work or is not practical, a symmetric main-secondary method can be used if both surfaces are element-based surfaces with deformable or deformable-made-rigid parent elements. To use this method, define two contact pairs using the same two surfaces, but switch the roles of main and secondary surface for the two contact pairs. This method causes Abaqus/Standard to treat each surface as a main surface and, thus, involves additional computational expense because contact searches must be conducted twice for the same contact pair. The increased accuracy provided by this method must be compared to the additional computational cost.

All of the contact formulations are available for symmetric main-secondary contact pairs, and can be applied using the same options discussed above.

Input File Usage

CONTACT PAIR, INTERACTION=interaction_property_name
surface_1, surface_2
surface_2, surface_1

Abaqus/CAE Usage

Interaction module: Create Interaction: Surface-to-surface
contact (Standard): select the main surface, click Surface, select the secondary surface
Copy this interaction to a new interaction, and edit the new interaction. In the interaction editor, click Switch to reverse the main and secondary surfaces.

Limitations of Symmetric Main-Secondary Contact Pairs

Using symmetric main-secondary contact pairs can lead to overconstraint problems when very stiff or hard contact conditions are enforced. See Contact Constraint Enforcement Methods in Abaqus/Standard for a discussion of overconstraints and alternate constraint enforcement methods.

For softened contact conditions, use of symmetric main-secondary contact pairs will cause deviations from the specified pressure-versus-overclosure behavior, because both contact pairs contribute to the overall interface stress without accounting for one another. For example, symmetric main-secondary contact pairs effectively double the overall contact stiffness if a linear pressure-overclosure relationship is specified.

Likewise, use of symmetric main-secondary contact pairs will cause deviations from the friction model if an optional shear stress limit is specified (see Using the Optional Shear Stress Limit), because the contact stresses observed by each contact pair will be approximately one-half of the total interface stress.

Similarly, it can be difficult to interpret the results at the interface for symmetric main-secondary contact pairs. In this case both surfaces at the interface act as secondary surfaces, so each has contact constraint values associated with it. The constraint values that represent contact pressures are not independent of each other. Therefore, the constraint values reported in the data (.dat) and results (.fil) files represent only a part of the total interface pressure and have to be summed to obtain the total.

In the output database, mechanical contact variables are reported at the nodes on both the main and secondary surfaces per contact pair and not just the secondary surface where constraints are formed. Consequently, two result sets are available per surface of a symmetric main-secondary contact pair; once when a surface acts as a secondary and once as a main. For nodal contact pressures the Visualization module of Abaqus/CAE only reports the maximum of the two pressure values associated with a node when the surface containing the node acts either as a main or as a secondary surface. Even in this case, the contact pressures do not represent the true interface pressure.

Apart from contact pressures, some contact output may be confusing with symmetric main-secondary contact pairs. For example, Abaqus/Standard may report a positive opening distance on one side of a contact interface but zero opening distance (i.e., touching) on the opposite side of the interface. Typically this is caused by the shape or relative mesh refinement of the two surfaces.

Defining Self-Contact

Define contact between a single surface and itself by specifying only a single surface or by specifying the same surface twice. The small-sliding tracking approach cannot be used with self-contact.

Defining Self-Contact Using Node-to-Surface Discretization

Abaqus/Standard uses node-to-surface contact discretization by default for self-contact.

Input File Usage

Use either of the following options:

CONTACT PAIR, INTERACTION=interaction_property_name
surface_1,

CONTACT PAIR, INTERACTION=interaction_property_name
surface_1, surface_1

Abaqus/CAE Usage

Interaction module: Create Interaction: 
Self-contact (Standard): select the surface
Interaction editor, Discretization method: Node to surface, Contact interaction property: interaction_property_name

Interaction module: Create Interaction: Surface-to-surface contact (Standard): select the surface, click Surface, select the surface again
Interaction editor, Sliding formulation: Finite sliding, Discretization method: Node to surface, Contact interaction property: interaction_property_name

Defining Self-Contact Using Surface-to-Surface Discretization

Surface-to-surface discretization often leads to more accurate modeling of self-contact simulations. However, because the self-contact surface is acting as both a main and a secondary, surface-to-surface discretization can sometimes significantly increase the solution cost.

Input File Usage

Use either of the following options:

CONTACT PAIR, INTERACTION=interaction_property_name, 
TYPE=SURFACE TO SURFACE
surface_1,

CONTACT PAIR, INTERACTION=interaction_property_name, 
TYPE=SURFACE TO SURFACE 
surface_1, surface_1

Abaqus/CAE Usage

Interaction module: Create Interaction: 
Self-contact (Standard): select the surface
Interaction editor, Discretization method: Surface to surface, Contact interaction property: interaction_property_name

Interaction module: Create Interaction: Surface-to-surface contact (Standard): select the surface, click Surface, select the surface again
Interaction editor, Sliding formulation: Finite sliding, Discretization method: Surface to surface, Contact interaction property: interaction_property_name

Limitations of Self-Contact

Self-contact is valid only for mechanical surface interactions and is limited to finite sliding with element-based surfaces.

A node of a self-contact surface can be both a secondary node and a member of the main surface for two-dimensional self-contact using the surface-to-surface formulation and for all three-dimensional self-contact. In these cases the contact behavior is similar to symmetric main-secondary contact pairs, and the issues discussed in Using Symmetric Main-Secondary Contact Pairs to Improve Contact Modeling apply. Abaqus/Standard automatically applies some numerical softening to contact conditions in these cases, as discussed in Contact Constraint Enforcement Methods in Abaqus/Standard.

Direct enforcement of hard contact conditions is the default constraint enforcement method for two-dimensional self-contact using the node-to-surface formulation. In this case, each node adjacent to a vertex where a two-dimensional surface folds onto itself is automatically assigned a secondary or main role during the analysis. Since contact constraints directly resist penetrations at nodes that act as secondary nodes, there is some possibility of unresolved penetrations at nodes that only act as main nodes for two-dimensional self-contact using the node-to-surface formulation.

Selecting Surfaces Used in Contact Pairs

Methods for creating surfaces are discussed in Element-Based Surface Definition, Node-Based Surface Definition, and Analytical Rigid Surface Definition; those sections discuss general restrictions for the various surface types. Considerations related to surface characteristics for various contact formulations are discussed in Contact Formulations in Abaqus/Standard. Additional considerations for surfaces used in contact definitions are discussed below.

Orientation Considerations for Shell-Like Surfaces

Abaqus/Standard requires main contact surfaces to be single-sided for node-to-surface contact and for some surface-to-surface contact formulations (see Fundamental Choices Affecting the Contact Formulation for details). This requires that you consider the proper orientation for main surfaces defined on elements, such as shells and membranes, that have positive and negative directions. For node-to-surface contact the orientation of secondary surface normals is irrelevant, but for surface-to-surface contact the orientation of single-sided secondary surfaces is taken into consideration.

Double-sided element-based surfaces are allowed for the default surface-to-surface contact formulations, although they are not always appropriate for cases with deep initial penetrations. If the main and secondary surfaces are both double-sided, the positive or negative orientation of the contact normal direction will be chosen such as to minimize (or avoid) penetrations for each contact constraint. If either or both of the surfaces are single-sided, the positive or negative orientation of the contact normal direction will be determined from the single-sided surface normals rather than the relative positions of the surfaces.

When the orientation of a contact surface is relevant to the contact formulation, you must consider the following aspects for surfaces on structural (beam and shell), membrane, truss, or rigid elements:

Adjacent surface faces must have consistent normal directions. Abaqus/Standard will issue an error message if adjacent surface faces have inconsistent normals on a single-sided surface whose orientation is relevant to the contact formulation.
Except for initial interference fit problems (see Modeling Contact Interference Fits in Abaqus/Standard), the secondary surface should be on the same side of the main surface as the outward normal. If, in the initial configuration, the secondary surface is on the opposite side of the main surface as the outward normal, Abaqus/Standard will detect overclosure of the surfaces and may have difficulty finding an initial solution if the overclosure is severe. An improper specification of the outward normal will often cause an analysis to immediately fail to converge. Figure 1 illustrates the proper and improper specification of a main surface's outward normal.

Figure 1. Example of proper and improper main surface orientation.
Contact will be ignored with surface-to-surface discretization if single-sided secondary and main surfaces have normal directions that are in approximately the same direction (for example, contact will not be enforced if the dot product of the secondary and main surface normals is positive).

The following output from a data check analysis (see Abaqus/Standard and Abaqus/Explicit Execution) can be useful in identifying incorrectly oriented main surfaces:

Initial clearances can be displayed in Abaqus/CAE with a contour plot of the variable COPEN at increment 0 of the first step; initial overclosures correspond to negative clearances.
Abaqus/Standard provides a detailed printout of the model's initial contact state.

Surface Connectivity Restrictions

Certain connectivity restrictions apply to contact surfaces depending on the type of contact formulation. Surface connectivity restrictions for the various contact formulations are summarized in Table 1. As indicated in this table, the connectivity restrictions are sometimes different for main and secondary surfaces. Self-contact surfaces act as both main and secondary surfaces; therefore, if a restriction applies to either a main or secondary surface, it also applies to self-contact. The potential connectivity restrictions referred to in Table 1 are described below:

Table 1. Summary of which connectivity characteristics of element-based surfaces are allowed for various contact formulations.
Contact formulation	Connectivity characteristics
Contact formulation	Discontinuous(or 3D faces joined at only one node)	T-intersection
Finite-sliding, node-to-surface	Main: Not allowedSecondary: Allowed	Main: Not allowedSecondary: Allowed
Small-sliding, node-to-surface	Main: AllowedSecondary: Allowed	Main: Not allowedSecondary: Allowed
Finite-sliding, surface-to-surface	Main: AllowedSecondary: Allowed	Main: AllowedSecondary: Allowed
Small-sliding, surface-to-surface	Main: AllowedSecondary: Allowed	Main: AllowedSecondary: Allowed

Discontinuous surfaces: Discontinuous contact surfaces are allowed in many cases, but the main surface for finite-sliding, node-to-surface contact cannot be made up of two or more disconnected regions (they must be continuous across element edges in three-dimensional models or across nodes in two-dimensional models). Figure 2 shows examples of continuous surfaces, whereas Figure 3 and Figure 4 show examples of discontinuous surfaces. Figure 5 shows an automatically generated free surface resulting from the specification of an element set consisting of two disjointed groups of elements. The resulting surface is not continuous since it is composed of two disjoint open curves, so this surface would be invalid as a main surface for finite-sliding, node-to-surface contact.

Figure 2. Examples of continuous surfaces.

Figure 3. Example of a discontinuous 2D surface.

Figure 4. Example of a discontinuous 3D surface.

Figure 5. Example of a discontinuous surface resulting from automatic free surface generation with a disjoint element set.
Portions of three-dimensional surfaces joined at only one node: The finite-sliding, node-to-surface contact formulation also does not allow three-dimensional main surface faces to be joined at a single node (they must be joined across a common element edge). Figure 6 shows an example of a surface with two faces connected by a single node.

Figure 6. Example of a 3D surface with two faces sharing a single node.
Surfaces with T-intersections: In some cases a contact surface cannot have more than two surface faces sharing a common main node in two dimensions or a common main edge in three dimensions. For example, Figure 7 shows examples of surfaces with T-intersections, in which three faces share a common node in two dimensions or a common edge in three dimensions. While more than two surface faces can share a common secondary node in two dimensions or a common edge in three dimensions for node-to-surface formulations, the secondary faces must be single-sided, which precludes the most common T-intersection cases for node-to-surface formulations.

Figure 7. Examples of surfaces with T-intersections.

Analytical Rigid Surfaces

Analytical rigid surfaces are often effective for efficiently modeling curved, rigid geometries, as discussed in Analytical Rigid Surface Definition. For rare cases in which a very large number (thousands) of segments would be necessary to define an analytical rigid surface, better performance can be achieved with an element-based rigid surface (see Element-Based Surface Definition).

Three-Dimensional Beam and Truss Surfaces

Abaqus/Standard cannot use three-dimensional beams or trusses to form a main surface because the elements do not have enough information to create unique surface normals. However, these elements can be used to define a secondary surface. Two-dimensional beams and trusses can be used to form both main and secondary surfaces.

Beam section offsets, specified either as part of the beam cross section definition or through the BEAM SECTION OFFSET option, are neglected for contact interactions in Abaqus/Standard.

Edge-Based Surfaces

Edge-based surfaces (Element-Based Surface Definition) on three-dimensional shell elements cannot be used in a contact analysis in Abaqus/Standard.

Limitations of Node-Based Surfaces

Use node-based surfaces with caution when the contact property definition includes user-defined softened contact properties or thermal or electrical interactions because the contact constitutive behavior (which relies on accurate calculation of contact pressure, heat flux, or electric current) will not be enforced correctly unless the precise surface area is associated with each node. For details, see Contact Pressure-Overclosure Relationships, Thermal Contact Properties, or Electrical Contact Properties.

Removing and Reactivating Contact Pairs

You can temporarily remove contact pairs from a simulation, which may result in significant computational savings by eliminating unnecessary contact searches and updates of surface orientations during the simulation. Removal and reactivation of contact pairs is commonly used in complicated forming processes where multiple tools need to interact with the workpiece at different stages in the analysis. Step-dependent activation and deactivation are also supported for general contact when used as an alternative to contact pairs for modeling contact (see Deactivating and Reactivating Contact Interactions across Steps).

You cannot remove tied contact pairs from a simulation (see Defining Tied Contact in Abaqus/Standard).

Removing Contact Pairs

Removal of contact pairs is a useful technique for uncoupling components of an assembly until they should be brought together (such as tooling in manufacturing process simulations). Significant computational expense might be saved by removing a contact pair and introducing it at the proper time, thus eliminating the need to monitor the contact conditions except when they are relevant.

Input File Usage

MODEL CHANGE, TYPE=CONTACT PAIR, REMOVE
secondary_surface, main_surface

Repeat the data line as needed.

Abaqus/CAE Usage

Use one of the following options:

Interaction module: Create Interaction: surface-to-surface contact or self-contact interaction editor: toggle off Active in this step

Interaction module: interaction manager: select interaction, Deactivate

Removal of Contact Forces Associated with Closed Contact Pairs

If the surfaces are in contact when a contact pair is removed, Abaqus/Standard stores the corresponding contact forces (or heat fluxes if thermal interactions are present, or electrical currents if it is a coupled-thermal electrical analysis) for every node on each surface. Abaqus/Standard automatically ramps these forces (or heat fluxes or electrical currents) linearly down to zero magnitude during the removal step. Abaqus/Standard always removes the contact constraints for mechanical surface interactions instantaneously.

Care must be taken in removing contact pairs in transient procedures. In transient heat transfer, fully coupled temperature-displacement, or fully coupled thermal-electrical-structural analysis if the fluxes are high and the step is long, this ramping down may have the effect of cooling down or heating up the rest of the body. In dynamic analysis if the forces are high and the step is long, kinetic energy can be imparted to the remaining portion of the model. This problem can be avoided by removing the contact pairs in a very short transient step prior to the rest of the analysis. This step can be done in a single increment.

Using an Allowable Contact Interference to Deactivate Contact Pairs

A contact pair with mechanical contact interactions can be deactivated during an analysis by assigning a very large allowable contact interference to the contact pairs (see Modeling Contact Interference Fits in Abaqus/Standard). This method has the disadvantage of not reducing the computational cost of the analysis because the contact algorithm will still calculate the contact conditions for the contact pair in each increment.

Reactivating Contact Pairs

All contact pairs that will be used in a simulation must be created at the start of the analysis; they cannot be created once the simulation has begun. However, contact pairs can be created, removed at the start of the analysis in the first step, and then reactivated at a later point during the simulation.

In Abaqus/CAE you can create contact pairs in any step. If a contact pair is created in a step other than the initial step, Abaqus/CAE automatically deactivates the contact pair in the initial step and reactivates it in the step in which you created it.

Input File Usage

MODEL CHANGE, TYPE=CONTACT PAIR, ADD
secondary_surface, main_surface

Repeat the data line as needed.

Abaqus/CAE Usage

Interaction module: Create Interaction: surface-to-surface contact or self-contact interaction editor: toggle on Active in this step

Reactivating Overclosed Contact Pairs

When a contact pair is reactivated, the contact constraint becomes active immediately. In mechanical simulations it is possible for the surfaces of a contact pair to move such that they become overclosed while the contact pair is inactive. If this overclosure is too severe when the contact pair is reactivated, Abaqus/Standard may encounter convergence problems as it tries to enforce the suddenly activated contact constraint. To avoid such problems, you can specify a permissible interference value, v, for the contact pair that is larger than the overclosure for the contact pair. Abaqus/Standard will ramp v down to zero during the step. For details on specifying allowable interferences, see Modeling Contact Interference Fits in Abaqus/Standard.

Output

Output variables associated with the interaction of contact pairs fall into two categories: nodal variables (sometimes called constraint variables) and whole surface variables. In addition, Abaqus outputs an array of diagnostic information associated with contact interactions, as discussed in Contact Diagnostics in an Abaqus/Standard Analysis.

For more detailed discussions of variables associated with thermal, electrical, and pore fluid analyses, see the sections on the related contact properties in Contact Property Models.

Nodal Contact Variables

Nodal contact variables can be contoured on contact surfaces in the Visualization module of Abaqus/CAE. Nodal contact variables include contact pressure and force, frictional shear stress and force, relative tangential motion (slip) of the surfaces during contact, clearance between surfaces, heat or fluid flux per unit area, fluid pressure, and electrical current per unit area. Many of the nodal contact variables written to the output database (.odb) file are often available for all contact nodes, regardless of whether they act as secondary or main nodes. Other nodal contact variables are available only at nodes acting as secondary nodes. Most contact output to the data (.dat) file, results (.fil) file, and the utility subroutine GETVRMAVGATNODE is associated with individual constraints. For contact output to the output database (.odb) file, some filtering is applied to reduce contact output noise.

The contact pressure distribution is of key interest in many Abaqus analyses. You can view the contact pressure on all contact surfaces except for analytical rigid surfaces and discrete rigid surfaces based on rigid-type elements (the latter restriction does not apply to general contact). You can view a contour plot of the contact pressure error indicator next to a contour plot of the contact pressure to gain perspective on local accuracy of the contact pressure solution in regions where the contact pressure solution is of interest (see Selection of Error Indicators Influencing Adaptive Remeshing for further discussion of error indicator output).

In some cases you may observe the contact pressure extending beyond the actual contact zone due to the following factors:

The contour plots are constructed by interpolating nodal values, which can cause nonzero values to appear within portions of facets outside of the contact region. For example, this effect is often noticeable at corners, such as when two same-sized, aligned blocks are in contact—if the contact surfaces wrap around the corners, the contact pressure contours will extend slightly around the corners.
Abaqus/Standard outputs postprocessed contact stresses to the output database. During postprocessing, nodal contact stresses are calculated as weighted averages of values associated with active contact constraints in which the node participates. For example, a main node can participate in multiple constraints whose connectivities contain the node. Similarly, a secondary node can participate in multiple constraints, as in the case of the finite sliding surface-to-surface formulation when more than one constraint is created at secondary node locations that are corners and edge features.

The weighting depends on the contact constraint area and a scaling factor based on the strength of the participation of the node in a constraint. The weighted averaging is intended to reduce contact stress noise. Modifications are made for calculating weightings, for example, at the corner nodes of quadratic faces (with zero consistent nodal areas) and main nodes that are outside the active contact region but participate in contact weakly through an active contact constraint. These modifications also have a filtering effect in terms of reducing contact stress values reported for nodes on the fringe of the active contact region. For such locations, contact nodal areas that are simply cumulative scaled constraint areas across constraints in which a node participates do not have much bearing on contact stress values.

In addition to averaging and filtering, contact stresses are also smoothed during the postprocessing operations. However, this filtering and subsequent smoothing are not "perfect" and can result in the contact zone size appearing somewhat exaggerated. Similarly, contact status output is also affected at nodes that lie on the fringe of the active contact region. In such cases, the contact status may be reported as closed at nodes in the exaggerated region even though it is open.

Due to these factors, trying to infer the contact force distribution from the contact stress distribution can be somewhat misleading. Instead, you can request nodal contact force output, which accurately represents the contact force distribution present in the analysis.

Whole Surface Variables

Whole surface variables are attributes of an entire secondary surface. Available as history output, these variables record the total force and moment due to contact pressure and frictional stress, the center of pressure and frictional stress (defined as the point closest to the centroid of the surface that lies on the line of action of the resultant force for which the resultant moment is minimal), and the total contact area (defined as the sum of all the facets where there is contact force). The last letter of each variable name (except the variable CAREA) denotes which contact force distribution on the surface is used to calculate the resultant:

N: Normal contact forces are used to derive the resultant quantity.
S: Shear contact forces are used to derive the resultant quantity.
T: The sum of the normal and shear contact forces is used to derive the resultant quantity.

For example, CFN is the total force due to contact pressure, CFS is the total force due to frictional stress, and CFT is the total force due to both contact pressure and frictional stress.

Each total moment output variable will not necessarily equal the cross product of the respective center of force vector and resultant force vector. Forces acting on two different nodes of a surface may have components acting in opposite directions, such that these nodal force components generate a net moment but not a net force; therefore, the total moment may not arise entirely from the resultant force. The center of force output variables tend to be most meaningful when the surface nodal forces act in approximately the same direction.

Requesting Output

Certain contact variables must be requested as a group. For example, to output the clearance between surfaces (COPEN), you must request the variable CDISP (contact displacements). CDISP outputs both COPEN and CSLIP (tangential motion of the surfaces during contact). A complete listing of available contact pair variables and identifiers is given in Abaqus/Standard Output Variable Identifiers.

Output requests can be limited to individual contact pairs or portions of a secondary surface. You can:

request output associated with a given contact pair;
request output associated with a given secondary surface, including contributions from all of the contact pairs to which the secondary surface belongs; and
limit the output by specifying a node set containing a subset of the nodes on the secondary surface.

Instructions on forming these output requests are available in the following sections:

To request output to the data (.dat) file, see Surface Output from Abaqus/Standard.
To request output to the output database (.odb) file, see Writing Surface Output to the Output Database.

Differences for Small-Sliding and Finite-Sliding Contact

For small-sliding contact problems the contact area is calculated in the input file preprocessor from the undeformed shape of the model; thus, it does not change throughout the analysis, and contact pressures for small-sliding contact are calculated according to this invariant contact area. This behavior is different from that in finite-sliding contact problems, where the contact area and contact pressures are calculated according to the deformed shape of the model.

Output of Tangential Results

Abaqus reports the values of tangential variables (frictional shear stress, viscous shear stress, and relative tangential motion) with respect to the local tangent directions defined on the surfaces. The local tangent directions CTANDIR1 and CTANDIR2 can be output by requesting the generic output variable CTANDIR. The definition of local tangent directions is explained in Local Tangent Directions on a Surface. These directions do not always correspond to the global coordinate system, and they rotate with the contact pair in a geometrically nonlinear analysis.

Abaqus/Standard calculates tangential results at each constraint point by taking the scalar product of the variable's vector and a local tangent direction, $t_{1}$ or $t_{2}$ , associated with the constraint point. The number at the end of a variable's name indicates whether the variable corresponds to the first or second local tangent direction. For example, CSHEAR1 is the frictional shear stress component in the first local tangent direction, while CSHEAR2 is the frictional shear stress component in the second local tangent direction.

Definition of Accumulated Incremental Relative Motion (Slip)

Abaqus/Standard defines the incremental relative motion (also known as slip) as the scalar product of the incremental relative nodal displacement vector and a local tangent direction. The incremental relative nodal displacement vector measures the motion of a secondary node relative to the motion of the main surface. The incremental slip is accumulated only when the secondary node is contacting the main surface. The sums of all such incremental slips during the analysis are reported as CSLIP1 and CSLIP2. Details about the calculation of this quantity can be found in Small-sliding interaction between bodies, Finite-sliding interaction between deformable bodies, and Finite-sliding interaction between a deformable and a rigid body.

Extending the Range for Which Contact Opening Output Is Provided for Gaps

To reduce computational costs, detailed computations to monitor potential points of interaction are avoided by default where surfaces are separated by a distance greater than the minimum gap distance at which contact forces (or thermal fluxes, etc.) may be transmitted. Therefore, contact opening (COPEN) output is typically not provided for finite-sliding contact where surfaces are opened by more than a small amount compared to surface facet dimensions. You can extend the range in which Abaqus/Standard provides contact opening output; COPEN will be provided up to gap distances equal to a specified “tracking thickness.” Using this control may increase computational cost due to extra contact tracking computations, especially if you specify a large tracking thickness value.

Input File Usage

SURFACE INTERACTION, TRACKING THICKNESS=value

Abaqus/CAE Usage

You cannot adjust the default tracking thickness in Abaqus/CAE.

Output for Axisymmetric Models

In an axisymmetric analysis the total forces and moments transmitted between the contacting bodies as a result of contact pressure and frictional stress are computed in the same manner as in a two-dimensional analysis. Therefore, the component of the total forces along the r-axis is nonzero, and the components of the total moments include contributions from the total forces along the r-axis.

Obtaining the “Maximum Torque” That Can Be Transmitted about the Z-Axis in an Axisymmetric Analysis

When modeling surface-based contact with axisymmetric elements (element types CAX and CGAX), Abaqus/Standard can calculate the maximum torque (output variable CTRQ) that can be transmitted about the z-axis. This capability is often of interest when modeling threaded connectors (see Axisymmetric analysis of a threaded connection). The maximum torque, T, is defined as

T = \int \int r^{2} p d s d θ,

where p is the pressure transmitted across the interface, r is the radius to a point on the interface, and s is the current distance along the interface in the r–z plane. This definition of “torque” effectively assumes a friction coefficient of unity.

Whole Model Contact-Related Energy Variables

For contact pairs, the same contact-related energy variables are available in Abaqus/Standard as for general contact, as described in Whole Model Contact-Related Energy Variables.