Finite-sliding interaction between deformable bodies

Abaqus/Standard provides a finite-sliding formulation to model the interaction between two deformable bodies where separation and sliding of finite amplitude and arbitrary rotation of the surfaces may arise. The formulation for two-dimensional and axisymmetric analysis, as well as for tube-in-tube analysis, is discussed in this section.

This page discusses:

Two-dimensional and axisymmetric slide line elements
Tube-tube interface elements
Slide line smoothing
Self contact

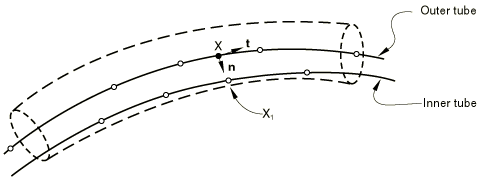
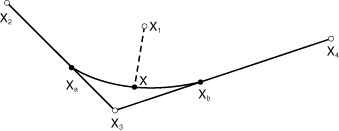
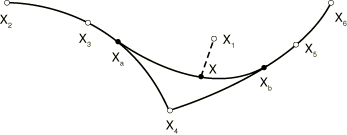
Two-dimensional and axisymmetric slide line elements

Consider contact of a node on the secondary surface $n_{1}$ with a segment of the main surface described by nodes $n_{2}$ , $n_{3}$ , $\dots$ , where the number of nodes depends on the order of the segment. For a linear segment the number of nodes is 2, whereas for a quadratic segment the number of nodes is 3. For a smoothed section of a linear slide line, the number of nodes is also 3; and for a smoothed section of a quadratic slide line, the number of nodes is 5. If the contact occurs at the (convex) vertex of two segments, only a single node will enter the equations. A typical linear segment is shown in Figure 1, and a quadratic segment is displayed in Figure 2. Smoothed segments are shown later in this section.

To derive the equations governing these elements, we consider the coordinates in the plane of the slide line. For the axisymmetric elements, this plane coincides with the two-dimensional space. First, we determine the point $x$ on the segment closest to the point $x_{1}$ on the secondary surface. We also determine the normal $n$ and tangent $t$ to the segment at that point. The point $x$ and the normal $n$ can be related to the overclosure $h$ with the relation

\begin{matrix} (1) & n h = x - x_{1} . \end{matrix}

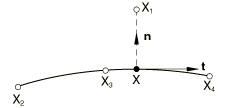
Since $x$ is on the segment, its position is defined completely by the interpolation function $N_{i}$ for the segment, the position $g$ , and the position $x_{i}$ of the nodes $n_{i}$ that are part of the segment. That allows us to write for Equation 1

\begin{matrix} (2) & n h = N_{i} (g) x_{i}, \end{matrix}

where $N_{1} = - 1$ and $N_{2}$ , $N_{3}$ , $\dots$ are functions of $g$ . For instance, for a linear segment you obtain $N_{2} = \frac{1}{2} (1 - g)$ , $N_{3} = \frac{1}{2} (1 + g)$ . For a quadratic segment you use $N_{2} = \frac{1}{2} g (g - 1)$ , $N_{3} = 1 - g^{2}$ , $N_{4} = \frac{1}{2} g (g + 1)$ . Similar expressions are obtained for smoothed segments of the slide line. The tangent $t$ to the slide line at point $x$ follows with

\begin{matrix} (3) & t \overset{def}{=} \frac{d x}{d s} = \frac{d x}{d g} / | \frac{d x}{d g} |, \end{matrix}

where

\frac{d x}{d g} = \frac{d N_{i}}{d g} x_{i} .

The position of point $x$ is determined from the condition that the normal and tangent must be orthogonal, which leads to the following equation for $g$ :

n \cdot t = N_{i} (g) \frac{d N_{j} (g)}{d g} x_{i} \cdot x_{j} = 0.

For linear segments this yields a linear equation, which can be solved directly. For quadratic and cubic segments it leads to third- or fifth-order equations, which must be solved iteratively. The equation is solved using Newton's method preceded by a number of bisections to find the true minimum distance solution.

To obtain the contact/slip equation, the position equation (Equation 2) is linearized. This linearization yields

δ n h + n δ h = \frac{d N_{i}}{d g} x_{i} δ g + N_{i} δ x_{i} = t δ s + N_{i} δ x_{i},

where $δ s$ is the slip. In the direction of contact, $n,$ this yields

\begin{matrix} (4) & δ h = N_{i} n \cdot δ x_{i}; \end{matrix}

and in the direction of slip, $t,$ one finds

δ s = - N_{i} t \cdot δ x_{i} - h t \cdot δ n .

It is assumed that slip is relevant only if the node $x_{1}$ is on the slide line; hence, it will be assumed that $h = 0$ . From this follows

\begin{matrix} (5) & δ s = - N_{i} t \cdot δ x_{i} . \end{matrix}

To obtain the initial stress stiffness terms, the second variations of $h$ and $s$ must be calculated. From Equation 4 follows

\begin{matrix} (6) & d δ h = δ x_{i} \cdot n \frac{d N_{i}}{d g} d g + N_{i} δ x_{i} \cdot d n . \end{matrix}

The first term is expressed readily in terms of $d x_{i}$ with the help of Equation 5:

\begin{matrix} (7) & \frac{d N_{i}}{d g} d g = \frac{d N_{i}}{d g} \frac{d g}{d s} \frac{d s}{d g} d g = \frac{d N_{i}}{d s} d s = - \frac{d N_{i}}{d s} N_{j} t \cdot d x_{j} . \end{matrix}

The rate of change of the normal can be re-expressed as

\begin{matrix} (8) & d n = (n n + t t) \cdot d n = t t \cdot d n = - t n \cdot d t . \end{matrix}

In this equation $n \cdot d t$ can be obtained from Equation 3:

\begin{matrix} (9) & \begin{matrix} n \cdot d t = ​ & n \cdot d (\frac{d x}{d g} ∕ | \frac{d x}{d g} |) = n \cdot (x_{i} \frac{d^{2} N_{i}}{d g^{2}} d g + \frac{d N_{i}}{d g} d x_{i}) ∕ | \frac{d x}{d g} | \\ = & - ρ_{n} d s + \frac{d N_{i}}{d s} n \cdot d x_{i} = ρ_{n} N_{i} t \cdot d x_{i} + \frac{d N_{i}}{d s} n \cdot d x_{i}, \end{matrix} \end{matrix}

where use was made of Equation 5 and $ρ_{n}$ (the segment curvature) is defined as

\begin{matrix} (10) & ρ_{n} \overset{def}{=} - n \cdot \frac{d^{2} x}{d g^{2}} / {| \frac{d x}{d g} |}^{2} . \end{matrix}

For straight segments $ρ_{n}$ obviously vanishes. Substitution of Equation 7 to Equation 9 in Equation 6 yields the final result:

\begin{matrix} (11) & d δ h = - δ x_{i} \cdot (n \frac{d N_{i}}{d s} N_{j} t + t N_{i} \frac{d N_{j}}{d s} n + t N_{i} ρ_{n} N_{j} t) \cdot d x_{j} . \end{matrix}

This expression is symmetric, as should be expected. The second variation in $s$ can be derived along similar lines:

\begin{matrix} (12) & d δ s = - δ x_{i} \cdot t \frac{d N_{i}}{d g} d g - N_{i} δ x_{i} \cdot d t . \end{matrix}

\begin{matrix} (13) & d t = (n n + t t) \cdot d t = n n \cdot d t . \end{matrix}

Substitution of Equation 7, Equation 9, and Equation 13 in Equation 12 yields

\begin{matrix} (14) & d δ s = δ x_{i} \cdot (t \frac{d N_{i}}{d s} N_{j} t - n N_{i} \frac{d N_{j}}{d s} n - n N_{i} ρ_{n} N_{j} t) \cdot d x_{j} . \end{matrix}

This expression is nonsymmetric.

The second variations of $h$ and $s$ vanish if no slip in the slide plane occurs $(d s = δ s = 0) .$

Tube-tube interface elements

In the case of tube-tube interface elements it is assumed that the inner tube can be considered the secondary surface and the outer tube the main surface. The tube-tube interface elements differ from the axisymmetric slide line elements in two ways. In the first place there is assumed to be a finite clearance between the tubes, which has the effect that the separation distance $h$ is finite even when contact occurs. In the second place for the three-dimensional element ITT31 there is a second possible local tangent direction in the plane of the cross-section of the tubes. The derivations for the ITT elements follow much along the same line as the derivations for the ISL elements. The contact equation can be written in the form

\begin{matrix} (15) & - n (h + h_{o}) = x_{1} - x . \end{matrix}

Here $x$ is a point on the outer tube that potentially contacts point $x_{1}$ on the inner tube, as shown in Figure 3.

In this equation $h_{o}$ is the (positive) radial clearance between the tubes. In a similar way as was done for the ISL elements, the contact equation can be written in the form

\begin{matrix} (16) & n (h + h_{o}) = - N_{i} (g) x_{i} . \end{matrix}

The sign reversal as compared to Equation 2 is related to the internal nature of the contact as compared to the external nature for the regular slide line elements. The linearized form of Equation 16 is

δ n (h + h_{o}) + n δ h = - t δ s - N_{i} δ x_{i} .

As before, we assume that during contact $h = 0$ . In the contact direction this yields

\begin{matrix} (17) & δ h = - N_{i} n \cdot δ x_{i}, \end{matrix}

and in the direction along the pipe,

\begin{matrix} (18) & δ s = - h_{o} t \cdot δ n - N_{i} t \cdot δ x_{i} . \end{matrix}

With use of $n \cdot t = 0$ , it readily follows

\begin{matrix} (19) & t \cdot δ n = - n \cdot δ t = ρ_{n} δ s - \frac{d N_{i}}{d s} n \cdot δ x_{i}, \end{matrix}

which transforms Equation 18 into

\begin{matrix} (20) & δ s = \frac{1}{1 + ρ_{n} h_{o}} (- N_{i} t \cdot δ x_{i} + h_{o} \frac{d N_{i}}{d s} n \cdot δ x_{i}), \end{matrix}

where $ρ_{n}$ is the segment curvature as defined by Equation 10. For the three-dimensional tube-tube interface element, one can define the transverse local tangent direction $s \overset{def}{=} t \times n$ , which yields

\begin{matrix} (21) & δ s_{2} = - N_{i} s \cdot δ x_{i} (= h_{o} s \cdot δ n) . \end{matrix}

The initial stress stiffness terms are again obtained by taking the second variations in $h_{o}$ , $s$ , and $s_{2}$ . From Equation 17 follows

\begin{matrix} (22) & d δ h = ρ_{n} δ s d s - δ s \frac{d N_{i}}{d s} n \cdot d x_{i} - δ x_{i} \cdot n \frac{d N_{i}}{d s} d s + h_{o} δ n \cdot d n, \end{matrix}

and with Equation 19 and Equation 21 follows

\begin{matrix} (23) & d n = tt \cdot d n + s s \cdot d n = t ρ_{n} d s - \frac{d N_{i}}{d s} n \cdot d x_{i} . \end{matrix}

Substitution of Equation 20 and Equation 23 in Equation 22 yields

\begin{matrix} (24) & \begin{matrix} d δ h = ρ_{n} (1 + h_{o} ρ_{n}) δ s d s \\ - & δ s (1 + h_{o} ρ_{n}) \frac{d N_{i}}{d s} n \cdot d x_{i} \\ - & δ x_{i} \cdot n \frac{d N_{i}}{d s} (1 + h_{o} ρ_{n}) d s \\ + & h_{o} δ x_{i} \cdot n \frac{d N_{i}}{d s} \frac{d N_{j}}{d s} n \cdot d x_{j} \\ + & \frac{δ s_{2} d s_{2}}{h_{o}} \end{matrix} \end{matrix}

This expression is symmetric. In the $t$ -direction the virtual work term has the form

F_{t} (δ s + h_{o} t \cdot δ n) \overset{def}{=} F_{t} δ \bar{s},

which yields with Equation 18

\begin{matrix} (25) & δ \bar{s} = - N_{i} t \cdot δ x_{i} . \end{matrix}

For the second variation follows

\begin{matrix} (26) & d δ \bar{s} = h_{o} δ n \cdot d t - t \cdot δ x_{i} \frac{d N_{i}}{d s} d s - t \cdot δ n d h - δ h t \cdot d n . \end{matrix}

\begin{matrix} (27) & \begin{matrix} d t & = d (\frac{d x}{d s}) = \frac{d^{2} x}{d g^{2}} d g ∕ | \frac{d x}{d g} | - \frac{d x}{d g} \frac{d x}{d g} \cdot \frac{d^{2} x}{d g^{2}} d g ∕ | \frac{d x}{d g} |^{3} \\ ​ = \frac{d N_{i}}{d s} (I - t t) \cdot d x_{i} + \frac{d^{2} x}{d g^{2}} ∕ {| \frac{d x}{d g} |}^{2} \cdot (I - t t) d s \\ ​ = \frac{d N_{i}}{d s} (n n + s s) \cdot d x_{i} - (ρ_{n} n + ρ_{s} s) d s, \end{matrix} \end{matrix}

where the transverse segment curvature $ρ_{s}$ is defined by

\begin{matrix} (28) & ρ_{s} \overset{def}{=} - s \cdot \frac{d^{2} x}{d g^{2}} / {| \frac{d x}{d g} |}^{2} . \end{matrix}

In this expression the terms involving $s$ vanish for element type ITT21. Substitution of Equation 20 and Equation 27 in Equation 26 yields

\begin{matrix} (29) & \begin{matrix} d δ \bar{s} = δ s \cdot ( & - ρ_{s} d s + \frac{d N_{i}}{d s} s \cdot d x_{i}) \\ - δ x_{i} \cdot t \frac{d N_{i}}{d s} d s \\ - ρ_{n} δ s d h + δ x_{i} \cdot n \frac{d N_{i}}{d s} d h \\ - ρ_{n} δ h d s + δ h \frac{d N_{i}}{d s} n \cdot d x_{i} \end{matrix} \end{matrix}

In the $s$ -direction one simply looks at the first variation in $δ s_{2}$ :

\begin{matrix} (30) & d δ s_{2} = δ x_{i} \cdot (- s \frac{d N_{i}}{d s} d s - N_{i} d s) . \end{matrix}

d s = n n \cdot d s + t t \cdot d s = - n s \cdot d n - t s \cdot d t .

With Equation 20, Equation 23, and Equation 27 follows

d s = \frac{- n d s_{2}}{h_{o}} + t (ρ_{s} d s - \frac{d N_{i}}{ds} s \cdot d x_{i}) .

Substituted in Equation 30 this yields

\begin{matrix} (31) & \begin{matrix} d δ s_{2} = ​ & - δ x_{i} \cdot s \frac{d N_{i}}{d s} d s + N_{i} δ x_{i} \cdot n \frac{d s_{2}}{h_{0}} \\ + N_{i} δ x_{i} \cdot t (- ρ_{s} d s + \frac{d N_{j}}{d s} s \cdot d x_{j}) . \end{matrix} \end{matrix}

Slide line smoothing

At the junction of two segments along a slide line, a discontinuity in slope may occur. This discontinuity can cause convergence problems because during iteration a contact point might move back and forth between two segments. Hence, it is useful to smooth the transition between segments. Consider first the transition between two linear segments (Figure 4).

The junction of the two segments is connected by a Hermitian polynomial between the points $x_{a}$ and $x_{b}$ , which are located on the segments:

x_{a} = α x_{2} + (1 - α) x_{3}, x_{b} = α x_{4} + (1 - α) x_{3} .

The positions of $x_{a}$ and $x_{b}$ are, hence, determined by the smoothing factor $α$ , which is specified directly by the user in the range $0 \leq α \leq 0.5$ .

We choose $g$ as the parameter coordinate on the smoothed segment, with $- 1 \leq g \leq 1$ . At the extreme values for $g$ the coordinates are $x_{a}$ and $x_{b}$ , and for the coordinate derivatives we choose

\frac{d x_{a}}{d g} = x_{3} - x_{a} = α (x_{3} - x_{2}), \frac{d x_{b}}{d g} = x_{b} - x_{3} = α (x_{4} - x_{3}) .

With the Hermitian interpolation functions we can calculate the position $x$ of a point on the segment as a function of $g$ :

\begin{matrix} x = ​ & \frac{1}{4} (g^{3} - 3 g + 2) x_{a} + \frac{1}{4} (- g^{3} + 3 g + 2) x_{b} \\ + & \frac{1}{4} (g^{3} - g^{2} - g + 1) \frac{d x_{a}}{d g} + \frac{1}{4} (g^{3} + g^{2} - g - 1) \frac{d x_{b}}{d g} . \end{matrix}

Combining the above equations yields

\begin{matrix} (32) & x = \frac{α}{4} (g^{2} - 2 g + 1) x_{2} + \frac{1}{4} (4 - 2 α (g^{2} + 1)) x_{3} + \frac{α}{4} (g^{2} + 2 g + 1) x_{4} . \end{matrix}

The smoothing has in fact been done with a second-order polynomial. In the formulation of the interface contact and friction equations, the treatment of a smoothing segment is identical to the treatment of a regular segment. A transition between quadratic segments is shown in Figure 5.

It is readily established that in this case

\begin{matrix} x_{a} & ​ = (2 α^{2} - α) x_{2} + (- 4 α^{2} + 4 α) x_{3} + (1 - 3 α + 2 α^{2}) x_{4}, \\ x_{b} & ​ = (2 α^{2} - α) x_{6} + (- 4 α^{2} + 4 α) x_{5} + (1 - 3 α + 2 α^{2}) x_{4} . \end{matrix}

For the coordinate derivatives we choose

\begin{matrix} \frac{d x_{a}}{d g} & = - α \frac{d x_{a}}{d α} = (α - 4 α^{2}) x_{2} + (- 4 α + 8 α^{2}) x_{3} + (3 α - 4 α^{2}) x_{4}, \\ \frac{d x_{b}}{d g} & = α \frac{d x_{b}}{d α} = (- α + 4 α^{2}) x_{6} + (4 α - 8 α^{2}) x_{5} + (- 3 α + 4 α^{2}) x_{4} . \end{matrix}

As before, $α$ is specified directly by the user. Substitution of these equations in the Hermite shape functions yields

\begin{matrix} (33) & \begin{matrix} x = \frac{1}{4} (α & [- 2 α g^{3} + (4 α - 1) g^{2} + (- 2 α + 2) g - 1] x_{2} \\ + α [4 α g^{3} + (- 8 α + 4) g^{2} + (4 α - 8) g + 4] x_{3} \\ + [(8 α^{2} - 6 α) g^{2} + (- 6 α + 4)] x_{4} \\ + α [- 4 α g^{3} + (- 8 α + 4) g^{2} + (- 4 α + 8) g + 4] x_{5} \\ + α [2 α g^{3} + (4 α - 1) g^{2} + (2 α - 2) g - 1] x_{6}) . \end{matrix} \end{matrix}

If $x_{3} = \frac{1}{2} (x_{2} + x_{4})$ and $x_{5} = \frac{1}{2} (x_{4} + x_{6})$ , the equations reduce to the same equations as were used for smoothing between linear segments.

For the transition between a linear segment with nodes $x_{2}$ and $x_{4}$ and a quadratic segment with nodes $x_{4}$ , $x_{5}$ , and $x_{6}$ the formulas become

\begin{matrix} x_{a} & ​ = α x_{2} + (1 - α) x_{4}, \\ x_{b} & ​ = (2 α^{2} - α) x_{6} + (- 4 α^{2} + 4 α) x_{5} + (1 - 3 α + 2 α^{2}) x_{4} . \end{matrix}

The coordinate derivatives are

\begin{matrix} \frac{d x_{a}}{d g} & = x_{4} - x_{a} = α (x_{4} - x_{2}), \\ \frac{d x_{b}}{d g} & = α \frac{d x_{b}}{d α} = (- α + 4 α^{2}) x_{6} + (4 α - 8 α^{2}) x_{5} + (- 3 α + 4 α^{2}) x_{4} . \end{matrix}

As a result,

\begin{matrix} (34) & \begin{matrix} x = \frac{1}{4} (α & [g^{2} - 2 g + 1] x_{2} \\ + [2 α^{2} g^{3} + (4 α^{2} - 4 α) g^{2} + (2 α^{2} - 4 α) g + (4 - 4 α)] x_{4} \\ + α [- 4 α g^{3} + (- 8 α + 4) g^{2} + (- 4 α + 8) g + 4] x_{5} \\ + α [2 α g^{3} + (4 α - 1) g^{2} + (2 α - 2) g - 1] x_{6}) . \end{matrix} \end{matrix}

For the transition between a quadratic segment with nodes $x_{2}$ , $x_{3}$ , and $x_{4}$ and a linear segment with nodes $x_{4}$ and $x_{6}$ , the formulas become

\begin{matrix} x_{a} & ​ = (2 α^{2} - α) x_{2} + (- 4 α^{2} + 4 α) x_{3} + (1 - 3 α + 2 α^{2}) x_{4}, \\ x_{b} & ​ = α x_{6} + (1 - α) x_{4} . \end{matrix}

The coordinate derivatives are

\begin{matrix} \frac{d x_{a}}{d g} & = - α \frac{d x_{a}}{d α} = (α - 4 α^{2}) x_{2} + (- 4 α + 8 α^{2}) x_{3} + (3 α - 4 α^{2}) x_{4}, \\ \frac{d x_{b}}{d g} & = x_{b} - x_{4} = α (x_{6} - x_{4}) . \end{matrix}

As a result,

\begin{matrix} (35) & \begin{matrix} x = \frac{1}{4} (α & [- 2 α g^{3} + (4 α - 1) g^{2} + (- 2 α + 2) g - 1] x_{2} \\ + α [4 α g^{3} + (- 8 α + 4) g^{2} + (4 α - 8) g + 4] x_{3} \\ + [- 2 α^{2} g^{3} + (4 α^{2} - 4 α) g^{2} - (2 α^{2} - 4 α) g + (4 - 4 α)] x_{4} \\ + α [g^{2} + 2 g + 1] x_{6}) . \end{matrix} \end{matrix}

Compared to pure linear-to-linear and quadratic-to-quadratic segment transitions, in both mixed linear-to-quadratic and quadratic-to-linear cases, only the junction node $x_{4}$ terms change.

Self contact

Self contact is available in the context of a surface folding and touching itself. Appropriate contact elements are generated internally for each node on the surface. A node is allowed to contact all of the surface segments, with the exception of the segments that are adjacent to the node. Since a node is simultaneously a main and a secondary (producing symmetric main-secondary relationships), overconstraints would occur, for example, if the meshes on both sides of the interface matched exactly. If only a pair of nodes matches in two dimensions, no problem occurs due to the smoothing carried out on the main side of the interface. To avoid solver problems due to overconstraining, three-dimensional self-contact is activated only if penalty-type contact is used.

The mathematical treatment of contact elements is the same as described above, with a few modifications in two dimensions. When two adjacent segments of the surface fold forming a sharp crack, the contact algorithm becomes pure main-secondary instead of symmetric to prevent redundant contact constraints. It has been arbitrarily chosen that of these two segments the shortest is the secondary and the longest is the main.