Two
Abaqus
methods that are particularly useful for analyzing threaded connectors are the
specification of an allowable contact interference and of pressure penetration
loads.
The automatic “shrink” fit method can be used to automatically resolve
the overclosure of two contacting surfaces. This method is applicable only
during the first step of an analysis, and it cannot be used with self-contact.
See
Modeling Contact Interference Fits in Abaqus/Standard
for details.
The surface-based pressure penetration capability described in Fluid Pressure Penetration Loads is used to simulate pressure penetration between
contacting surfaces. This capability is provided for simulating cases where a joint
between two deforming bodies (for example, between two components threaded onto each
other) or between a deforming body and a rigid surface (such as a soft gasket used in a
joint) is exposed at one or multiple ends to a fluid pressure. This pressure will
penetrate into the joint and load the surfaces forming the joint until some area of the
surfaces is reached where the contact pressure between the abutting surfaces exceeds the
critical value specified in the pressure penetration load, cutting off further
penetration.
The contact output variables in
Abaqus
can provide the designer a wealth of information about the performance of a
connector during all steps of an analysis. When modeling surface-based contact
with axisymmetric elements (CAX- and CGAX-type elements) an output quantity of particular use is the
maximum torque that can be transmitted about the z-axis by
a specified contact pair. The maximum torque, T, is a
scalar value defined as
where p is the pressure transmitted across the interface,
r is the radius to a point on the interface, and s
is the current distance along the interface in the
r–z plane. T is not a real
torque; it is a computed limit of torque that a contact pair may transmit about the
z-axis assuming that all the secondary nodes on the contact surface are
slipping and that the friction coefficient is set to 1. The actual maximum torque that can be
transmitted about the z-axis by a specified contact pair can be estimated
by scaling T by the friction coefficient specified for the contact pair.
The value of T can be output by requesting the contact output variable
CTRQ.
This example demonstrates the usefulness of the specification of allowable
contact interference and of pressure penetration loads as well as the
Abaqus
contact output variables in an axisymmetric analysis of a particular threaded
connector.
Geometry and model
A three-dimensional cut-away view of the threaded connection assembly
analyzed in this example is shown in
Figure 1.
Although the actual threads are helical, they are represented with an
axisymmetric geometry. Previous experience has shown this simplification to be
appropriate for these types of problems. Both the “pin” and the “box” are made
from steel with a Young's modulus of 207 GPa (30 × 106 psi) and a
Poisson's ratio of 0.3, which is characterized by a von Mises plasticity model.
The unthreaded section of the pin has inner and outer radii of 48.6 mm (1.913
in) and 57.2 mm (2.25 in), respectively. The major diameter of the threads on
the pin (diameter measured at the crest of the threads) is slightly larger than
the major diameter of the threads on the box (diameter measured at the roots of
the threads); thus, there is an initial interference between the threads on the
pin and on the box.
The deformed axisymmetric mesh (after the initial interference has been
resolved) in the vicinity of the threads is illustrated in
Figure 2.
Contact is modeled by the interaction of contact surfaces defined by grouping
specific faces of the elements in the contacting regions.
Loading and boundary conditions
Two analyses of the threaded connection are performed: an axisymmetric
analysis using CAX4 elements and an axisymmetric analysis with twist using CGAX4 elements. The first four steps for the two analyses are
identical. The CGAX4 model has an additional fifth step.
The initial interference fit of the threads on the pin and box is resolved
in the first step using the automatic “shrink” fit method with a friction
coefficient of 0. In the second step the assembly is held fixed while the
friction coefficient is changed from 0 to 0.1 using changes to friction
properties. An internal gauge pressure of 0.689 MPa (100 psi) is applied to the
connector in the third step. The pressure on the contact surfaces is applied
using pressure penetration loading. In the first three steps the displacements
in the 2-direction are constrained to be zero at both ends of the assembly. To
simulate an axial load in the fourth step, a displacement boundary condition of
−0.254 cm (−0.1 in) is applied to the end of the box in the 2-direction. In the
fifth step for the CGAX4 model the end of the pin is held fixed while the end of the box
is rotated 0.1 radians about the 2-axis, simulating a torque being applied to
the connector. The actual torques generated about the 2-axis by the frictional
stresses in the fifth step are given by the output variable CMS2. This value is compared to the estimated value given by CTRQ for the fourth step.
Results and discussion
All analyses are performed as large-displacement analyses. The results from the first four steps
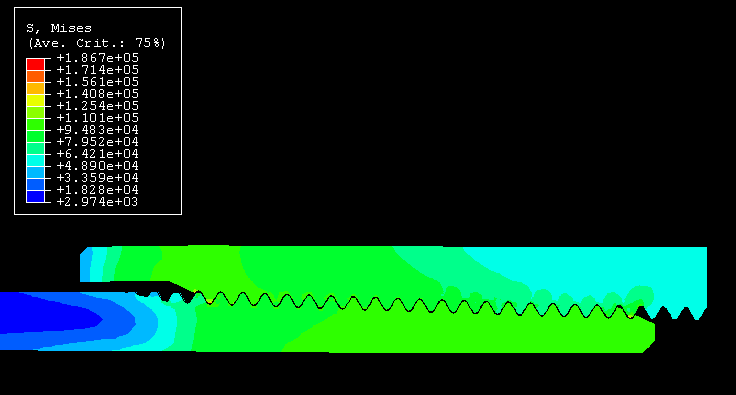
for both models are identical. Figure 3 and Figure 4, respectively, show the von Mises stress distributions in the threaded assembly after the
overclosure has been resolved in Step 1 and after the displacement boundary condition has
been applied in Step 4. As is illustrated in Figure 4, some of the threads on the pin are beginning to pull out at the end of Step 4. However,
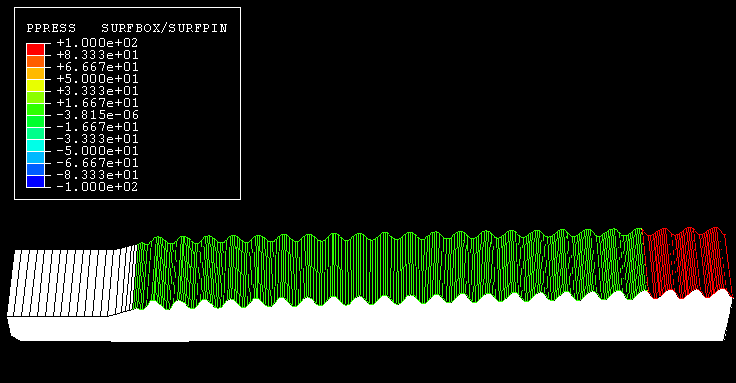
plots of the pressure penetration on the contact surface of the box in Figure 5 and Figure 6 show that the seal of the threads is maintained; thus, no leakage is indicated. If the
seal had failed, the penetration pressure on the box surface in contact with the pin would
be 0.689 MPa (100 psi) instead of 0. Other contact output variables such as
CPRESS and
COPEN provide additional information about
the contact state throughout the analysis.
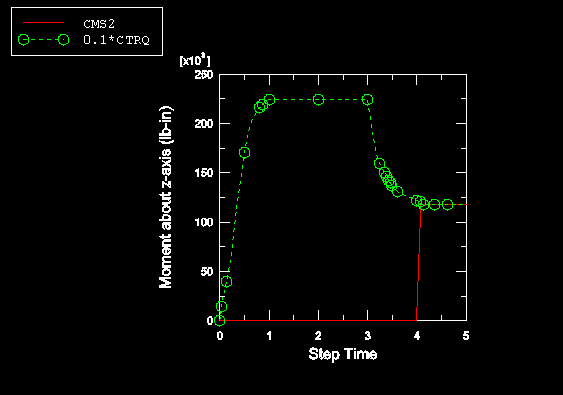
The scaled values of CTRQ (scaled by the friction coefficient of 0.1) and the values of CMS2 for all five steps in the CGAX4 analysis are illustrated in
Figure 7.
The value of CTRQ at the end of Step 4 is 1.22 × 106 lb-in, which
translates into an estimated maximum torque of 1.22 × 105 lb-in for
a friction coefficient of 0.1. The value of CMS2 computed during Step 5 for the CGAX4 model is 1.18 × 105 lb-in. The 3.7% difference in this
example between the predicted and actual torque values can be attributed to a
slight change in the normal pressure distribution between the contact surfaces
that occurs when the box is rotated. The value of CMS2 is zero for the first four steps since no frictional stresses
are generated between the contact surfaces until the fifth step. The value of CTRQ increases in the first step as the overclosure is resolved and
dips in the fourth step due to the change in the contact pressure as the box is
pulled away from the pin (see
Figure 7).