Elastic Behavior of Porous Materials

The porous elastic model in Abaqus/Standard is used to study porous materials with nonlinear pressure-dependent elastic behavior (including logarithmic or power laws). This form of nonlinear elasticity is valid for small elastic strains.

The porous elastic models:

are used to study the pressure-dependent elastic behavior of materials;
include a logarithmic model and a power law–based model; and
can have properties that depend on temperature and other field variables.

This page discusses:

Logarithmic Porous Elasticity Model
Power Law–Based Porous Elasticity Model
Material Options
Elements

Logarithmic Porous Elasticity Model

The logarithmic porous elasticity model is valid for small elastic strains (normally less than 5%). It is a nonlinear, isotropic elasticity model in which the pressure stress varies as an exponential function of volumetric strain. The model allows a zero or nonzero elastic tensile stress limit.

Defining the Volumetric Behavior

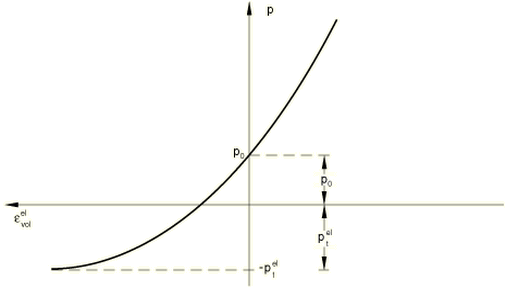
Often, the elastic part of the volumetric behavior of porous materials is modeled accurately by assuming that the elastic part of the change in volume of the material is proportional to the logarithm of the pressure stress (Figure 1):

\frac{κ}{(1 + e_{0})} \ln (\frac{p_{0} + p_{t}^{e l}}{p + p_{t}^{e l}}) = J^{e l} - 1,

where $κ$ is the “logarithmic bulk modulus”; $e_{0}$ is the initial void ratio; p is the equivalent pressure stress, defined by

p = - \frac{1}{3} trace σ = - \frac{1}{3} (σ_{11} + σ_{22} + σ_{33});

$p_{0}$ is the initial value of the equivalent pressure stress; $J^{e l}$ is the elastic part of the volume ratio between the current and reference configurations; and $p_{t}^{e l}$ is the “elastic tensile strength” of the material (in the sense that $J^{e l} \to \infty$ as $p \to - p_{t}^{e l}$ ).

Input File Usage

Use all three of the following options to define a porous elastic material:

POROUS ELASTIC, TYPE=LOGARITHMIC,SHEAR=G or POISSON to define  $κ$  and  $p_{t}^{e l}$  
INITIAL CONDITIONS, TYPE=STRESS to define  $p_{0}$  
INITIAL CONDITIONS, TYPE=RATIO to define  $e_{0}$

Abaqus/CAE Usage

Use all three of the following options to define a porous elastic material:

Property module: material editor: MechanicalElasticityPorous Elastic: Type: Logarithmic

Load module: Create Predefined Field: Step: Initial: choose Mechanical for the Category and Stress for the Types for Selected Step

Load module: Create Predefined Field: Step: Initial: choose Other for the Category and Void ratio for the Types for Selected Step

Defining the Shear Behavior

The deviatoric elastic behavior of a porous material can be defined in either of two ways.

By Defining the Shear Modulus

Give the shear modulus, G. The deviatoric stress, $S$ , is then related to the deviatoric part of the total elastic strain, $e^{e l}$ , by

S = 2 G e^{e l} .

In this case the shear behavior is not affected by compaction of the material.

Input File Usage

POROUS ELASTIC, TYPE=LOGARITHMIC,SHEAR=G

Abaqus/CAE Usage

Property module: material editor: MechanicalElasticityPorous Elastic: Type: Logarithmic: Shear: G

By Defining Poisson's Ratio

Define Poisson's ratio, $ν$ . The instantaneous shear modulus is then defined from the instantaneous bulk modulus and Poisson's ratio as

G = \frac{3 (1 - 2 ν) (1 + e_{0})}{2 (1 + ν) κ} (p + p_{t}^{e l}) \exp (ε_{v o l}^{e l}),

where $ε_{v o l}^{e l} = \ln J^{e l}$ is the logarithmic measure of the elastic volume change. In this case

d S = 2 G d e^{e l} .

Thus, the elastic shear stiffness increases as the material is compacted. This equation is integrated to give the total stress–total elastic strain relationship.

Input File Usage

POROUS ELASTIC, TYPE=LOGARITHMIC, SHEAR=POISSON

Abaqus/CAE Usage

Property module: material editor: MechanicalElasticityPorous Elastic: Type: Logarithmic: Shear: Poisson

Power Law–Based Porous Elasticity Model

In the case of the power law–based porous elasticity model, Young's modulus is related to the pressure by a power law:

E = E_{r e f} {[\frac{p + p_{0}}{p_{r e f} + p_{0}}]}^{n} p > 0; E = f E_{r e f} p \leq 0,

where $E_{r e f}$ is the reference Young's modulus at pressure $p_{r e f}$ , and $p_{0}$ and $n$ are material constants. $f$ is used to define the elastic modulus for tensile effective pressure and is calculated as follows:

f = {[\frac{p_{0}}{p_{r e f} + p_{0}}]}^{n} .

Poisson's ratio is an exponential function of pressure

ν = ν_{0} + (ν_{\infty} - ν_{0}) (1 - e^{- m p}) p > 0; ν = ν_{0} p \leq 0,

where $ν_{\infty}$ is the value of the Poisson's ratio corresponding to the limit $p \to \infty$ , $ν_{0}$ is the value of the Poisson's ratio at $p = 0$ , and $m$ is a material constant.

Material Options

The porous elasticity models can be used by themselves or in combination with other material options.

The logarithmic porous elasticity model can be combined with:

the Extended Drucker-Prager Models;
the Modified Drucker-Prager/Cap Model;
the Critical State (Clay) Plasticity Model; or
isotropic expansion to introduce thermal volume changes (Thermal Expansion).

The power law–based porous elasticity model can be combined with:

the soft rock plasticity model; or
isotropic expansion to introduce thermal volume changes (Thermal Expansion).

It is not possible to use porous elasticity with rate-dependent plasticity or viscoelasticity.

Porous elasticity cannot be used with the porous metal plasticity model (Porous Metal Plasticity).

See Combining Material Behaviors for more details.

Elements

Porous elasticity cannot be used with hybrid elements or plane stress elements (including shells and membranes), but it can be used with any other pure stress/displacement element in Abaqus/Standard.

If used with reduced-integration elements with total-stiffness hourglass control, Abaqus/Standard cannot calculate a default value for the hourglass stiffness of the element if the logarithmic porous elasticity model is used and the shear behavior is defined through Poisson's ratio. Hence, you must specify the hourglass stiffness. See Section Controls for details.

If fluid pore pressure is important (such as in undrained soils), stress/displacement elements that include pore pressure can be used.