Connector Stops and Locks

Connector stops and locks can be:

  • specified in any connector with available components of relative motion;

  • used to specify contact-enforced stops in individual components of relative motion; and

  • used to lock in position an available component of relative motion when a certain criterion is met.

This page discusses:

See Also
About Connectors
Connector Behavior
In Other Guides
*CONNECTOR BEHAVIOR
*CONNECTOR LOCK
*CONNECTOR STOP
Defining a stop
Defining a lock

Products Abaqus/Standard Abaqus/Explicit Abaqus/CAE

Defining Connector Stops

In the physical construction of most connectors, the admissible position of one body relative to the other is limited by a certain range. In Abaqus these limits are modeled as built-in inequality constraints. You specify the available components of relative motion for which the connector stops are to be defined and the lower and upper limit values of the connector's admissible range of positions in the directions of the components of relative motion.

Input File Usage

Use the following options to define a connector stop:

CONNECTOR BEHAVIOR, NAME=name
CONNECTOR STOP, COMPONENT=component number
lower limit, upper limit

Abaqus/CAE Usage

Interaction module: connector section editor: AddStop: Components: component or components, Lower bound: lower limit, Upper bound: upper limit

Example

Since the shock in Figure 1 has finite length, contact with the ends of the shock determines the upper and lower limit values of the distance that node b can be from node a.

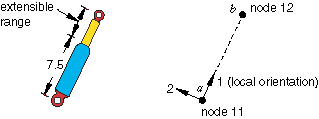
Figure 1. Simplified connector model of a shock absorber.

Assume that the maximum length of the shock is 15.0 units and that the minimum length is 7.5 units. Modify the input file presented in About Connectors that is associated with the example in Figure 1 to include the following lines: 

CONNECTOR BEHAVIOR, NAME=sbehavior
...
CONNECTOR STOP, COMPONENT=1
7.5, 15.0

Defining Connector Locks

Connector mechanisms might have devices designed to lock the connector in place once a desired configuration is achieved. For example, a revolute connection might have a falling-pin mechanism that locks the rotational motion after achieving a desired angle. A user-defined connector locking criterion can be defined for connector elements that contain available components of relative motion. You can select the component of relative motion for which the locking criterion is defined.

Connector locks can be used to specify connector behavior for constrained as well as available components of relative motion. Limit values for force or moment can be specified for all components of relative motion involved in the connection. The force/moment used in evaluating the criterion is as computed in the output variable CTF. In addition, limit values can be specified for relative position corresponding to the available components of relative motion. If no other behavior is specified for an available component of relative motion, a force locking criterion will not be useful because CTF is zero.

In Abaqus/Explicit you can also specify the limiting values of velocity in the available components as a criterion for locking. Velocity-dependent locking criteria are useful in modeling seatbelt systems in automobiles (see Seat belt analysis of a simplified crash dummy). Moreover, the limiting values can be dependent on temperature and field variables. Field variable dependencies can be used to model time-dependent locks.

If the locking criterion specified for the selected component of relative motion is met, either all components lock or a single available component locks in place. By default, all components of relative motion are locked in place upon meeting the locking criterion. In this case the connector element will be completely kinematically locked from that point on. In dynamic analyses this locking may introduce high accelerations. You can specify if only a selected component of relative motion is locked.

Input File Usage

Use the following options to define a connector lock:

CONNECTOR BEHAVIOR, NAME=name
CONNECTOR LOCK, COMPONENT=component number, 
LOCK=ALL or component number

Abaqus/CAE Usage

Interaction module: connector section editor: AddLock: Components: component or components, Lock: All or Specify component

Example

In the example in Figure 1 assume that relative rotations about the shock will lock if the force in the local 3-direction exceeds 500.0 units of force. 

CONNECTOR BEHAVIOR, NAME=sbehavior
CONNECTOR LOCK, COMPONENT=3, LOCK=4
, , -500.0, 500.0

Defining Connector Stops and Locks in Linear Perturbation Procedures

The status of connector locks or stops cannot change during a linear perturbation analysis; all connector stop and connector lock definitions remain in the same status as in the base state.

Limitations

Activating a connector stop in a large-displacement analysis can require relatively small time increments so that the deformation history is continuous in the vicinity of the value of the relative motion at which you activated the stop. Large time increments can lead to a discontinuous deformation response that violates the connector stop.

An example of such a behavior is illustrated in Figure 2 in the context of a simple axial connector that is fixed at one end (node 1) and has an applied compressive load at the other end (node 2). Assume a specified connector stop behavior that is activated when the distance between the two nodes is half its initial value. If the compressive load is large enough and applied in a single increment, the displacement of node 2 can be so large that it ends up on the opposite side of node 1 (as shown in Figure 2), thereby violating the connector stop. Using smaller time increments would lead to a more continuous response that respects the specified connector stop behavior.

Figure 2. Scenario that could lead to violation of a connector stop specification.

Output

The Abaqus output variables available for connectors are listed in Abaqus/Standard Output Variable Identifiers and Abaqus/Explicit Output Variable Identifiers. The following output variables are of particular interest when defining stops and locks in connectors:

CSLST

Flags for connector stops and locks.

CRF

Connector reaction forces/moments.

At a given time and for a particular component of relative motion i, the output variable CSLSTi is 1 if the connector is actually stopped or locked in that component (stop or lock criteria are met). In that case, the correspondent CRF output variable will most likely be nonzero and equal to the actual force/moment required to enforce the stop or lock constraint. Since CRF is included in the calculation of CTF, the latter will change as well when the lock or stop is active.

If the stop or lock criteria are not met at a given time for a particular component i, the output variable CSLSTi is 0 and in most cases the correspondent reaction force CRF is zero (the only possible exception is when a connector motion is also applied in that component).