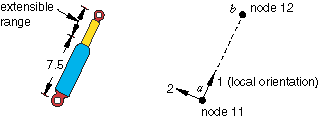
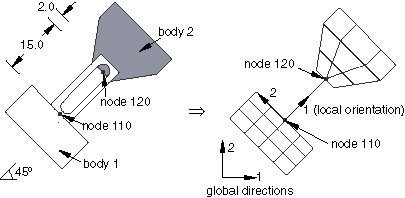
Typical Applications
The analyst is often faced with modeling problems in which two different parts are connected in some way. Sometimes connections are simple, such as two panels of sheet metal spot welded together or a door connected to a frame with a hinge. In other cases the connection may impose more complicated kinematic constraints, such as constant velocity joints, which transmit constant spinning velocity between misaligned and moving shafts. In addition to imposing kinematic constraints, connections may include (nonlinear) force versus displacement (or velocity) behavior in their unconstrained relative motion components, such as a muscle force resisting the rotation of a knee joint in a crash-test occupant model. More complex connections may include the following:
stopping mechanisms, which restrict the range of motion of an otherwise unconstrained relative motion;
internal friction, such as the lateral force or moments on a bolt generating friction in the translation of the bolt along a slot;
failure conditions, where excess force or displacement inside the connection causes the entire connection or a single component of relative motion to break free; and
locking mechanisms that engage after some force or displacement criteria is met, such as a snap-fit connector or a falling-pin locking mechanism on a satellite deployment arm.
In many situations the connection can be actuated either through displacement or force control, such as a hydraulic piston or a gear-driven robot arm.
In Abaqus/Standard if the two parts being connected are rigid bodies, multi-point constraints cannot be used to connect the bodies at nodes other than the reference nodes, since multi-point constraints use degree-of-freedom elimination and the other nodes on a rigid body do not have independent degrees of freedom. In Abaqus/Explicit this restriction does not apply. See General Multi-Point Constraints.
Connector elements in Abaqus provide an easy and versatile way to model these and many other types of physical mechanisms whose geometry is discrete (i.e., node-to-node), yet the kinematic and kinetic relationships describing the connection are complex.