Transient thermal loading of a viscoelastic slab

This example verifies the use of the time domain linear viscoelastic material model in conjunction with a temperature-time shift function.

This page discusses:

Problem description
Material
Analysis
Results and discussion
Input files
References
Figures

ProductsAbaqus/StandardAbaqus/Explicit

Problem description

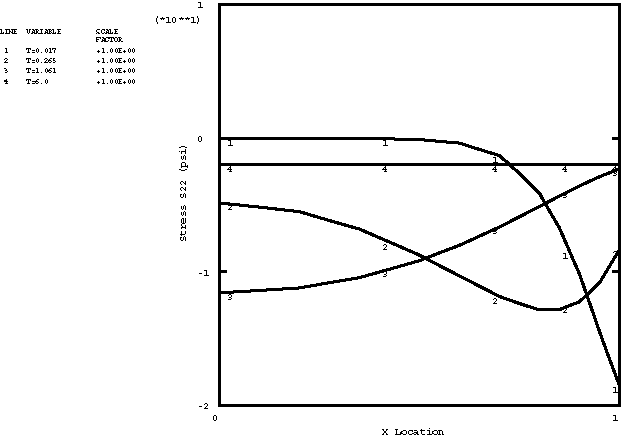
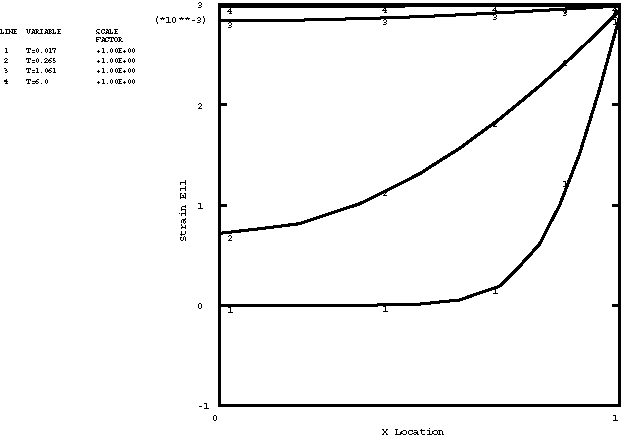
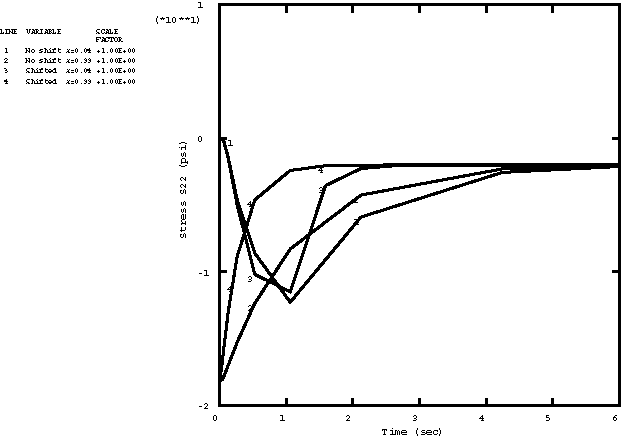
The example, taken from Collingwood et al. (1985), models a viscoelastic slab under plane strain restrained in all directions in its plane and examines the response of the slab after the temperature of its faces is raised suddenly to 100°.

The slab has unit half-thickness. Since the problem is one-dimensional, the slab is modeled with a single row of plane strain continuum elements. In Abaqus/Standard a sequential thermal-stress analysis is performed with two-dimensional, 8-node heat transfer elements, DC2D8, used for the heat transfer analysis and the corresponding 8-node plane strain continuum elements, CPE8R, used for the stress analysis. The mesh is shown in Figure 1. In Abaqus/Explicit a coupled thermal-stress analysis is performed using first-order plane strain elements (CPE3T and CPE4RT) to model the slab. Twenty elements are used along the length of the slab in the Abaqus/Explicit simulation.

The initial temperature throughout the slab is 0°. The outside face of the slab, at $X = $ 1, is instantaneously raised to 100°. The mesh (Figure 1) is finer toward $X = $ 1, where the temperature gradient is expected to be highest. The resulting transient temperature distribution is written to the results file and used as input to the subsequent stress analysis. Plane strain is imposed in the Y-direction by setting $u_{y} = $ 0 on the two faces of the mesh at $Y = $ 0 and $Y = $ 1. Symmetry about $X = $ 0 is also imposed.

Material

The thermal material properties are arbitrarily defined (in consistent units) as thermal conductivity (k) of 1.0, specific heat (c) of 1.0, and density ( $ρ$ ) of 1.0.

The viscoelastic material models (small-strain and large-strain) are the same as the ones used in Viscoelastic rod subjected to constant axial load, with the addition of a temperature-time shift. The temperature-time shift uses the Williams-Landel-Ferry approximation,

\log (A) = - \frac{C_{1} (θ - θ_{0})}{C_{2} + (θ - θ_{0})},

where $θ_{0}$ is the reference temperature at which the relaxation data are given and $C_{1}$ , $C_{2}$ are calibration constants obtained at this temperature (for additional information on the WLF equation, see Viscoelasticity). When $θ \leq θ_{0} - C_{2},$ the material behavior is elastic. In this example $C_{1} = $ 4.92, $C_{2} = $ 215.0°, and $θ_{0} = $ 70°. The coefficient of thermal expansion is 1.0 × 10⁻⁵ per degree.

Analysis

The transient heat transfer problem is analyzed in Abaqus/Standard using a heat transfer procedure for a time period of 6 seconds, so the structure is allowed to come to thermal equilibrium. The integration procedure used in Abaqus/Standard for transient heat transfer analysis introduces a relationship between the minimum usable time increment and the element size and material properties. The guideline given in Uncoupled Heat Transfer Analysis is

Δ t > \frac{ρ c}{6 k} Δ l^{2},

where $Δ l$ is the size of the smallest element in the mesh. If time increments smaller than this value are used, spurious oscillations may appear in the solution. Since the mesh is rather coarse, the minimum usable time increment predicted by the above formula is 4.17 × 10⁻⁴ seconds. A suggested initial time increment of 5 × 10⁻⁴ seconds is, therefore, used.

Automatic time incrementation is chosen by setting a value for the maximum temperature change allowed in an increment during a heat transfer analysis. Smaller values for the maximum temperature change cannot be used in this problem because they result in time increments that are smaller than the minimum usable time increment described above. As a consequence, the thermal analysis is rather approximate. A finer mesh would be necessary to obtain more accurate results.

The stress analysis uses the temperature distribution obtained in the heat transfer analysis to define the thermal loading. The quasi-static procedure (Quasi-Static Analysis) is used with automatic incrementation, chosen by specifying a value for the maximum difference in the creep strain increment over a time increment. This value is set to 2.0 × 10⁻³, which is of the same order of magnitude as the maximum elastic strain. The time period is 6 seconds, and the initial suggested time increment is 5.0 × 10⁻⁴ seconds to capture the high temperature gradients that occur very early in the analysis.

In Abaqus/Explicit the thermal and mechanical responses of the slab are determined simultaneously. The automatic time incrementation scheme available in Abaqus/Explicit is used to ensure numerical stability and to advance the solution in time.

Results and discussion

The temperature distribution in the first part of the problem is given in Carslaw and Yeager (1959). Table 1 compares that exact solution with the Abaqus results after an elapsed time of one second.

Table 1. Exact solution compared to Abaqus results.
$X / L$	Temperature
$X / L$	Carslaw and Yeager (1959)	Abaqus/Standard	Abaqus/Explicit
0.9	98.2	97.8	98.3
0.7	95.0	93.5	95.1
0.5	92.2	89.9	92.3
0.2	89.5	86.4	89.7
0.0	89.2	85.7	89.1

The Abaqus/Standard results are of limited accuracy because of the relatively large time increments used.

The stress and strain distributions at various times during the solution are shown in Figure 2 and Figure 3. The final stress in the slab is calculated as −0.0138 MPa (−2 psi), while the final strain is 2.99 × 10⁻³. Figure 4 shows the time history of the stress at the leftmost and rightmost integration points in the structure. Time histories for the same problem, solved without the temperature-time shift, are also shown in this figure. As expected, the shift considerably shortens the time required for the structure to reach equilibrium.

The equilibrium stress and strain distributions obtained from the stress analyses of the viscoelastic slab can be compared with those of an elastic slab whose properties correspond to the long-term properties of the viscoelastic material. The extensional relaxation function for the viscoelastic material is

\begin{matrix} E_{R} (t) & ​ = 69 (1 - 0.901001 (1 - e^{- t / 0.99})) MPa \\ or E_{R} (t) & ​ = 10000 (1 - 0.901001 (1 - e^{- t / 0.99})) psi . \end{matrix}

The long-term Young's modulus, $E_{L}$ , is $E_{R} (t \to \infty)$ and is 6.83 MPa (989.99 psi). The long-term Poisson's ratio can be calculated from the long-term Young's modulus and the bulk modulus,

ν_{L} = \frac{3 K - E_{L}}{6 K} = 0.4984.

The equilibrium values of $ε_{x x}$ and $σ_{y y}$ are obtained using linear elasticity

\begin{matrix} ε_{x x} & ​ = \frac{1}{E_{L}} (σ_{x x} - ν_{L} σ_{y y} - ν_{L} σ_{z z}) + α θ \\ ε_{y y} & ​ = \frac{1}{E_{L}} (σ_{y y} - ν_{L} σ_{z z} - ν_{L} σ_{x x}) + α θ . \end{matrix}

By symmetry $σ_{y y} = σ_{z z}$ , and by the assumptions of plane strain $ε_{y y} = ε_{z z} = $ 0. The slab is unrestrained in the X-direction, so $σ_{x x} = $ 0. These conditions result in stress and strain distributions that follow the temperature distribution,

σ_{y y} = - \frac{E_{L}}{1 - ν_{L}} α θ ε_{x x} = \frac{1 + ν_{L}}{1 - ν_{L}} α θ .

At steady state the temperature is 100° throughout the slab, so the final stress and strain are

σ_{y y} = - 0.0136 MPa = - 1.97 psi ε_{x x} = 2.99 \times 10^{- 3},

which agree with the steady-state values obtained in the analyses.

Input files

Abaqus/Standard input files

viscoslabthermload_heat.inp: Heat transfer analysis.
viscoslabthermload_smallstrain.inp: Small-strain analysis of the viscoelastic slab with the temperature-time shift included.
viscoslabthermload_largestrain.inp: Equivalent large-strain analysis.
viscoslabthermload_usr_utrs.inp: Stress analysis making use of user subroutine UTRS to define the WLF shift function. The solution using user subroutine UTRS is identical to that obtained from the job in viscoslabthermload_smallstrain.inp.
viscoslabthermload_usr_utrs.f: User subroutine UTRS used in conjunction with viscoslabthermload_usr_utrs.inp.
viscoslabthermload_postoutput.inp: POST OUTPUT analysis.

Abaqus/Explicit input files

viscoslabthermload_x_cpe3t.inp: Small-strain analysis of the viscoelastic slab with the temperature-time shift included; CPE3T elements.
viscoslabthermload_x_cpe4rt.inp: Small-strain analysis of the viscoelastic slab with the temperature-time shift included; CPE4RT elements.
viscoslabthermload_usr_cpe4rt.inp: Stress analysis making use of user subroutine VUTRS to define the WLF shift function. The solution using user subroutine VUTRS is identical to that obtained from the job in viscoslabthermload_x_cpe4rt.inp.
viscoslabthermload_usr_cpe4rt.f: User subroutine VUTRS used in conjunction with viscoslabthermload_usr_cpe4rt.inp.
viscoslabthermload_xh_cpe3t.inp: Large-strain analysis of the viscoelastic slab with the temperature-time shift included; CPE3T elements.
viscoslabthermload_xh_cpe4rt.inp: Large-strain analysis of the viscoelastic slab with the temperature-time shift included; CPE4RT elements.

To run the stress analyses without the shift, simply remove the TRS option and the one data line that follows it from viscoslabthermload_smallstrain.inp, viscoslabthermload_largestrain.inp, viscoslabthermload_x_cpe3t.inp, viscoslabthermload_x_cpe4rt.inp, viscoslabthermload_xh_cpe3t.inp, and viscoslabthermload_xh_cpe4rt.inp.

References

Carslaw, H. S., and J. C. Yeager, Conduction of Heat in Solids, Clarendon Press, Oxford, 1959.
Collingwood, G. A., E. B. Becker, and T. Miller, User's Manual for the TEXVISC Computer Program, Morton Thiokol, Inc., Document Numbers U-85-4550A and U-85-4550B, 1985.

Figures