Porous elasticity

The model is based on the experimental observation that in porous materials during elastic (recoverable) straining, the change in the void ratio—e—and the change in the logarithm of the equivalent pressure stress—p—defined as

are linearly related, so that in rate form,

where $\kappa$ is a material parameter. In this form the material has zero tensile strength. If the tensile strength $p_t^{el}$ is nonzero, the equivalent relation is

which includes the special case of zero tensile strength ($p_t^{el}=0$). It can be shown that, if the compressibility of the solid material is neglected, the volume change of a material sample is

where $e_0$ is the initial void ratio. If we define the elastic void ratio from the elastic volume change according to the relationship

and then integrate the linear relation, the volumetric elasticity relationship is

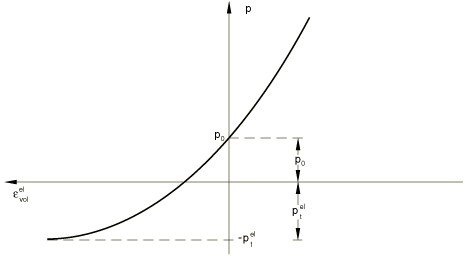
where $p_0$ is the initial pressure stress, prescribed by initial conditions. Note that for a zero tensile strength material it is required that $p_0>0$. This equation can be inverted to yield

as illustrated inFigure 1.

Figure 1. Porous elastic volumetric behavior.

The deviatoric elastic behavior is defined either by choosing a constant shear modulus, G, so that the deviatoric elastic stiffness is independent of the equivalent pressure stress or choosing a constant Poisson's ratio, $\nu$, so that the deviatoric elastic stiffness increases as the equivalent pressure stress increases. If a constant shear modulus is given, the deviatoric relationship is

whereas when Poisson's ratio is given, the relationship has the rate form

where

for a material with nonzero tensile strength. In these equations $\mathbf{S}$ is the deviatoric stress:

and ${\mathbf{e}}^{el}$ is the deviatoric part of the elastic strain:

where ${\epsilon }_{vol}^{el}$ is the volumetric part of the elastic strain.

In the case of the power law–based porous elasticity model, Young's modulus is related to the pressure by a power law:

where $E_{ref}$ is the reference Young's modulus at pressure $p_{ref}$ and $p_0$ and $n$ are material constants. $f$ is used to define the elastic modulus for tensile effective pressure and is calculated as follows:

Poisson's ratio is an exponential function of pressure

where ${\nu }_{\infty }$ is the value of the Poisson's ratio corresponding to the limit $p\to \infty$ , ${\nu }_0$ is the value of the Poisson's ratio at $p=0$ , and $m$ is a material constant.