Contact Damping

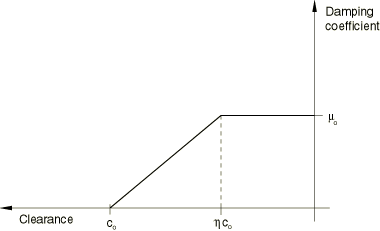
In Abaqus/Standard the damping coefficient, $\mu$, is a function of surface clearance, as shown in Figure 1. The damping coefficient is defined as a proportionality constant with units of pressure divided by velocity.

Figure 1. Damping coefficient-clearance relationship for viscous damping in Abaqus/Standard.

In Abaqus/Explicit the damping coefficient will remain at the specified constant value while the surfaces are in contact and at zero otherwise. The damping coefficient can be defined as a proportionality constant with units of pressure divided by velocity or as a unitless fraction of critical damping.

To define viscous damping, you must include it in a contact property definition.

SURFACE INTERACTION, NAME=interaction_property_name
CONTACT DAMPING

INTERFACE or GAP, ELSET=name
CONTACT DAMPING

Interaction module: contact property editor: MechanicalDamping

In Abaqus/Standard the appropriate magnitude for the local contact damping factor, ${\mu }_0$, is problem-dependent. In some cases a simple calculation can be used to determine the magnitude; in other cases a reasonable value for ${\mu }_0$ must be determined by trial and error. A reasonable value is one that has minimal impact on the solution prior to the unstable behavior in the model. A preliminary value can be found by looking at the contact pressures and velocities in the model before damping is added, as described below.

It may be difficult to determine the nodal velocities prior to the unstable behavior if output was not requested frequently. In such a situation the information in the message (.msg) file can be used to estimate the peak nodal velocity. By default, Abaqus/Standard provides the peak nodal displacement increment at every converged increment in this file. This displacement increment can be used along with the time increment to calculate a peak nodal velocity for the model. Although this velocity may not be very close to the actual relative velocity of the surfaces, it should be within an order of magnitude and is a reasonable value to use in calculating an initial viscous damping coefficient.

The maximum contact pressure between the surfaces also needs to be estimated. The viscous damping coefficient should then be set to a value that is a few orders of magnitude less than the ratio of the estimated maximum contact pressure over the calculated nodal velocity.

If it is not feasible to obtain the pressure and velocities as discussed above, a high damping value should be used initially and repeated analyses should be performed with smaller and smaller values. An appropriate value for ${\mu }_0$ is one that is large enough to enable the analysis to get past any unstable response but not so large that the results at earlier or later times are affected significantly. Snap-through buckling analysis of circular arches demonstrates how the magnitude of the damping coefficient can be determined using the methods explained above.

The following example outlines how the value might be chosen for a typical case. Consider a simple modification to the two-dimensional Euler column buckling problem: add rigid surfaces parallel and on either side of the column so that the beam will contact the surfaces when it buckles. As the axial load is increased beyond the buckling load, the column will flatten out against the surface. Then, the midpoint of contact will lift off the surface and the beam will buckle into a higher mode. Figure 2 shows this shape.

Figure 2. Constrained Euler buckling example for viscous damping.

When the column first buckles, the contact force, F, that the column exerts on one of the rigid surfaces can be approximated as

where h is the separation distance between the rigid surfaces, l is the beam length, P is the applied load, and $P_{crit}$ is the buckling load.

The approximation of the contact force entails the assumption that a single point comes into contact and that the shape of the buckled column does not change. The units of ${\mu }_0$ are contact force per velocity, assuming that a node-based surface is used in this model. The velocity of the column, v, at the point of contact can be approximated as

where $\mathrm{\Delta }t$ is the time increment. These estimates for the contact force and the column velocity give a value for the damping coefficient:

This value can be used as a starting value, but different values should be tested.