About the Element Library

Figure 1 shows the element families that are used most commonly in a stress analysis; in addition, continuum (fluid) elements are used in a fluid analysis. One of the major distinctions between different element families is the geometry type that each family assumes.

Figure 1. Commonly used element families.

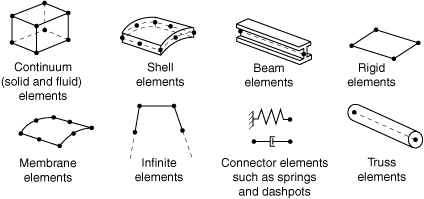
The first letter or letters of an element's name indicate to which family the element belongs. For example, S4R is a shell element, CINPE4 is an infinite element, and C3D8I is a continuum element.

The degrees of freedom are the fundamental variables calculated during the analysis. For a stress/displacement simulation the degrees of freedom are the translations and, for shell, pipe, and beam elements, the rotations at each node. For a heat transfer simulation the degrees of freedom are the temperatures at each node; for a coupled thermal-stress analysis temperature degrees of freedom exist in addition to displacement degrees of freedom at each node. Heat transfer analyses and coupled thermal-stress analyses therefore require the use of different elements than does a stress analysis since the degrees of freedom are not the same. See Conventions for a summary of the degrees of freedom available in Abaqus for various element and analysis types.

Displacements or other degrees of freedom are calculated at the nodes of the element. At any other point in the element, the displacements are obtained by interpolating from the nodal displacements. Usually the interpolation order is determined by the number of nodes used in the element.

• Elements that have nodes only at their corners, such as the 8-node brick shown in Figure 2(a), use linear interpolation in each direction and are often called linear elements or first-order elements.

• In Abaqus/Standard elements with midside nodes, such as the 20-node brick shown in Figure 2(b), use quadratic interpolation and are often called quadratic elements or second-order elements.

• Modified triangular or tetrahedral elements with midside nodes, such as the 10-node tetrahedron shown in Figure 2(c), use a modified second-order interpolation and are often called modified or modified second-order elements.

Figure 2. Linear brick, quadratic brick, and modified tetrahedral elements.

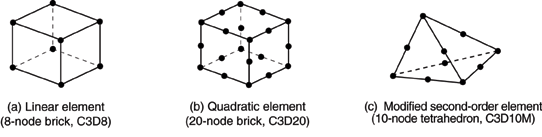
Typically, the number of nodes in an element is clearly identified in its name. The 8-node brick element is called C3D8, and the 4-node shell element is called S4R.

The beam element family uses a slightly different convention: the order of interpolation is identified in the name. Thus, a first-order, three-dimensional beam element is called B31, whereas a second-order, three-dimensional beam element is called B32. A similar convention is used for axisymmetric shell and membrane elements.

An element's formulation refers to the mathematical theory used to define the element's behavior. In the Lagrangian, or material, description of behavior the element deforms with the material. In the alternative Eulerian, or spatial, description elements are fixed in space as the material flows through them. Eulerian methods are used commonly in fluid mechanics simulations. Abaqus/Standard uses Eulerian elements to model convective heat transfer. Abaqus/Explicit also offers multimaterial Eulerian elements for use in stress/displacement analyses. Adaptive meshing in Abaqus/Explicit combines the features of pure Lagrangian and Eulerian analyses and allows the motion of the element to be independent of the material (see About ALE Adaptive Meshing). All other stress/displacement elements in Abaqus are based on the Lagrangian formulation. In Abaqus/Explicit the Eulerian elements can interact with Lagrangian elements through general contact (see Eulerian Analysis).

To accommodate different types of behavior, some element families in Abaqus include elements with several different formulations. For example, the conventional shell element family has three classes: one suitable for general-purpose shell analysis, another for thin shells, and yet another for thick shells. In addition, Abaqus also offers continuum shell elements, which have nodal connectivities like continuum elements but are formulated to model shell behavior with as few as one element through the shell thickness.

Some Abaqus/Standard element families have a standard formulation as well as some alternative formulations. Elements with alternative formulations are identified by an additional character at the end of the element name. For example, the continuum, beam, and truss element families include members with a hybrid formulation (to deal with incompressible or inextensible behavior); these elements are identified by the letter H at the end of the name (C3D8H or B31H).

Abaqus/Standard uses the lumped mass formulation for low-order elements; Abaqus/Explicit uses the lumped mass formulation for all elements. As a consequence, the second mass moments of inertia can deviate from the theoretical values, especially for coarse meshes.

In steady-state dynamic and frequency extraction procedures (see About Dynamic Analysis Procedures), Abaqus/Standard uses a special projected mass matrix algorithm for the S3, S3R, S4, S4R, SC6R, SC8R, and S4R5 shell elements. As a consequence, slight differences may be observed in models that contain these elements when comparing results from steady-state dynamic and frequency extraction procedures to those of an implicit dynamic analysis.

Abaqus uses numerical techniques to integrate various quantities over the volume of each element, thus allowing complete generality in material behavior. Using Gaussian quadrature for most elements, Abaqus evaluates the material response at each integration point in each element. Some continuum elements in Abaqus can use full or reduced integration, a choice that can have a significant effect on the accuracy of the element for a given problem.

Abaqus uses the letter R at the end of the element name to label reduced-integration elements. For example, CAX4R is the 4-node, reduced-integration, axisymmetric, solid element.

Shell, pipe, and beam element properties can be defined as general section behaviors; or each cross-section of the element can be integrated numerically, so that nonlinear response associated with nonlinear material behavior can be tracked accurately when needed. In addition, a composite layered section can be specified for shells and, in Abaqus/Standard, three-dimensional bricks, with different materials for each layer through the section.