Pattern-based eigenstrain analysis

The problem simulates the process of additive manufacturing of a cube of dimensions 20.0 × 20.0 × 20.0. The analyses use the special-purpose technique for pattern-based eigenstrain modeling of additive manufacturing processes in Abaqus/Standard (see Specifying Element Activation and Eigenstrain Using the Pattern-Based Method). Models using solid elements (C3D8) and shell elements (S4) are tested.

Model

Full element activation is applied to the cube to simulate the layer-upon-layer material deposition. The material layer thickness (slice height) is 1.0. A total of 20 layers is needed to build one cube.

Mesh

The cube is modeled with a mesh of 20 × 20 × 20 C3D8 elements or a mesh of 16800 S4 elements.

Material

A linear isotropic elastic material is used, with:

Young's modulus,	$E$=10000
Poisson's ratio,	$\upsilon$=0.33

(The units are not important.)

Loading

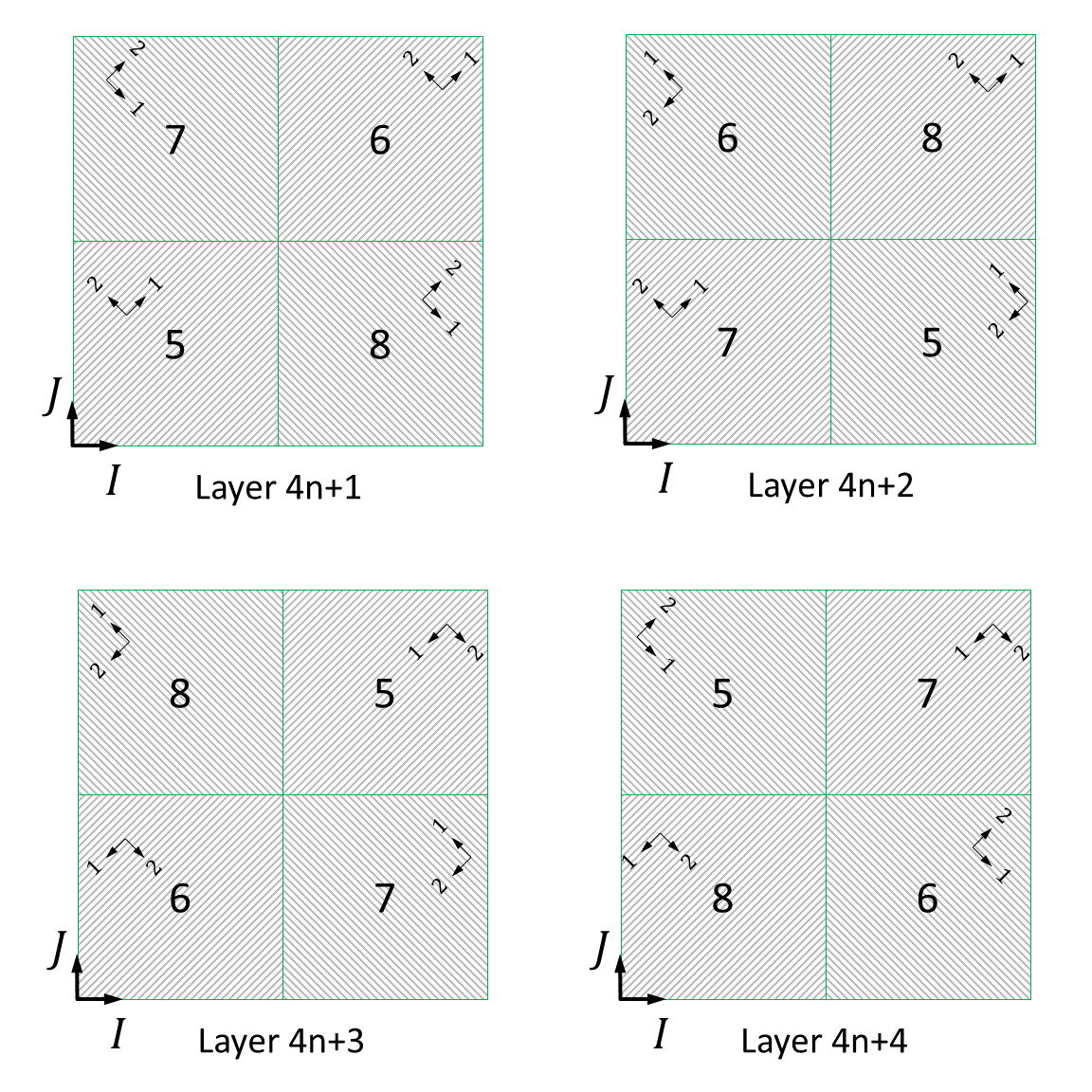
Different scan-pattern strategies are applied to build the lower half and the upper half of the cube, as shown in Figure 1 and Figure 2, respectively. Each scan pattern consists of four patches. The in-plane dimensions of all patches are 5.0 × 5.0. For the lower half of the cube the layer-to-layer (slice-to-slice) rotation of the scan pattern is defined as 0° about the K-axis of the build system I-J-K; namely, the first 10 layers have an identical eigenstrain pattern. The layer-to-layer rotation angle of the scan pattern of the upper half of the cube is 90°, which means that the eigenstrain pattern repeats every four layers.

The orientation of the build system I-J-K is defined to align with the global orientation X-Y-Z. The origin of the build system is at the bottom center of the cube.

Orthotropic eigenstrains are applied on element activation, ${\epsilon }_{12}^{*}={\epsilon }_{13}^{*}={\epsilon }_{23}^{*}=0$. Table 1 shows the value and the in-plane rotation angle of the eigenstrains for each patch. For solid elements (for example, C3D8 elements), the material orientation is updated to align with the rotation angle of the eigenstrain of the patch.

Table 1. Rotation angle and value of eigenstrains of each patch.

Patch No.	Local in-plane rotation	Eigenstrain component ${\epsilon }_{11}^{*}$	Eigenstrain component ${\epsilon }_{22}^{*}$	Eigenstrain component ${\epsilon }_{33}^{*}$
1	0°	-0.001	-0.001	-0.0005
2	0°	-0.002	-0.002	-0.0005
3	90°	-0.003	-0.003	-0.0005
4	90°	-0.004	-0.004	-0.0005
5	45°	-0.005	-0.005	-0.0005
6	45°	-0.006	-0.006	-0.0005
7	-45°	-0.007	-0.007	-0.0005
8	-45°	-0.008	-0.008	-0.0005

Boundary conditions

All degrees of freedom of the nodes on the bottom surface of the cube are fixed.