Uncoupled heat transfer analysis

The Abaqus/Standard capability for uncoupled heat transfer analysis is intended to model solid body heat conduction with general, temperature-dependent conductivity; internal energy (including latent heat effects); and quite general convection and radiation boundary conditions. This section describes the basic energy balance, constitutive models, boundary conditions, finite element discretization, and time integration procedures used.

This page discusses:

Energy balance
Constitutive definition
Boundary conditions
Spatial discretization
Time integration

Energy balance

The basic energy balance is (Green and Naghdi)

\begin{matrix} (1) & \int_{V} ρ \dot{U} d V = \int_{S} q d S + \int_{V} r d V, \end{matrix}

where V is a volume of solid material, with surface area S; $ρ$ is the density of the material; $\dot{U}$ is the material time rate of the internal energy; q is the heat flux per unit area of the body, flowing into the body; and r is the heat supplied internally into the body per unit volume.

It is assumed that the thermal and mechanical problems are uncoupled in the sense that $U = U (θ)$ only, where $θ$ is the temperature of the material, and q and r do not depend on the strains or displacements of the body. For simplicity a Lagrangian description is assumed, so “volume” and “surface” mean the volume and surface in the reference configuration.

Constitutive definition

This relationship is usually written in terms of a specific heat, neglecting coupling between mechanical and thermal problems:

c (θ) = \frac{d U}{d θ},

except for latent heat effects at phase changes, which are given separately in terms of solidus and liquidus temperatures (the lower and upper temperature bounds of the phase change range) and the total internal energy associated with the phase change, called the latent heat. When latent heat is given, it is assumed to be in addition to the specific heat effect (see Figure 1).

For many cases it is reasonable to assume that the phase change occurs within a known temperature range, which can be specified by the user. However, in some cases it may be necessary to include a kinetic theory for the phase change to model the effect accurately (an example would be the prediction of crystallization in a polymer casting process). For such cases the user can model the process in considerable detail, using the solution-dependent state variable feature in Abaqus, with user subroutine HETVAL.

Heat conduction is assumed to be governed by the Fourier law,

\begin{matrix} (2) & f = - k \frac{\partial θ}{\partial x}, \end{matrix}

where $k$ is the conductivity matrix, $k = k (θ)$ ; $f$ is the heat flux; and $x$ is position. The conductivity $k$ can be fully anisotropic, orthotropic, or isotropic.

Boundary conditions

Boundary conditions can be specified as prescribed temperature, $θ = θ (x, t)$ ; prescribed surface heat flux, $q = q (x, t)$ per area; prescribed volumetric heat flux, $q = r (x, t)$ per volume; surface convection: $q = - h (θ - θ^{0})$ , where $h = h (x, t)$ is the film coefficient and $θ^{0} = θ^{0} (x, t)$ is the sink temperature; and radiation: $q = {}^{-}A ({(θ - θ^{Z})}^{4} - {(θ^{0} - θ^{Z})}^{4})$ , where A is the radiation constant (emissivity times the Stefan-Boltzmann constant) and $θ^{Z}$ is the value of absolute zero on the temperature scale being used. Surfaces can also participate in cavity radiation effects. The cavity radiation formulation in Abaqus is described in Cavity radiation.

Spatial discretization

A variational statement of the energy balance, Equation 1, together with the Fourier law, Equation 2, is obtained directly by the standard Galerkin approach as

\begin{matrix} (3) & \int_{V} ρ \dot{U} δ θ d V + \int_{V} \frac{\partial δ θ}{\partial x} \cdot k \cdot \frac{\partial θ}{\partial x} d V = \int_{V} δ θ r d V + \int_{s_{q}} δ θ q d S, \end{matrix}

where $δ θ$ is an arbitrary variational field satisfying the essential boundary conditions. The body is approximated geometrically with finite elements, so the temperature is interpolated as

θ = N^{N} (x) θ^{N}, N = 1, 2, \dots,

where $θ^{N}$ are nodal temperatures. The Galerkin approach assumes that $δ θ$ , the variational field, is interpolated by the same functions:

δ θ = N^{N} δ θ^{N} .

First- and second-order polynomials in one, two, and three dimensions are used for the $N^{N}$ . With these interpolations the variational statement, Equation 3 becomes

\begin{matrix} δ θ^{N} {\int_{V} N^{N} ρ \dot{U} d V & + \int_{V} \frac{\partial N^{N}}{\partial x} \cdot k \cdot \frac{\partial θ}{\partial x} d V \\ = \int_{V} N^{N} r d V + \int_{S_{q}} N^{N} q d S}, \end{matrix}

and since the $δ θ^{N}$ are arbitrarily chosen, this gives the system of equations

\begin{matrix} (4) & \begin{matrix} \int_{V} N^{N} ρ \dot{U} d V & + \int_{V} \frac{\partial N^{N}}{\partial x} \cdot k \cdot \frac{\partial θ}{\partial x} d V \\ ​ = \int_{V} N^{N} r d V + \int_{S_{q}} N^{N} q d S . \end{matrix} \end{matrix}

This set of equations is the “continuous time description” of the geometric approximation.

Time integration

Abaqus/Standard uses the backward difference algorithm:

\begin{matrix} (5) & {\dot{U}}_{t + Δ t} = (U_{t + Δ t} - U_{t}) (1 / Δ t) . \end{matrix}

This operator is chosen for a number of reasons. First of all, we choose from one-step operators of the form

f_{t + Δ t} = f_{t} + ((1 - γ) {\dot{f}}_{t} + γ {\dot{f}}_{t + Δ t}) Δ t

because of their simplicity in implementation (for example, no special starting procedures are needed) and well-understood behavior. For $γ < 1 / 2$ such operators are only conditionally stable for linear heat transfer problems. We prefer to work with unconditionally stable methods, because Abaqus is most commonly applied to problems where the solution is sought over very long time periods (compared to the stability limit for the explicit form of the operator, $γ = 0$ ), and so choose $γ \geq 1 / 2$ . Of these operators the central difference method, $γ = 1 / 2$ , has the highest accuracy. However, that form of the operator tends to produce oscillations in the early time solution that are not present in the backward difference form. Thus, we use $γ = 1$ : backward difference. Introducing the operator, Equation 5, into the energy balance Equation 4 gives

\begin{matrix} (6) & \begin{matrix} \frac{1}{Δ t} & \int_{V} N^{N} ρ (U_{t + Δ t} - U_{t}) d V + \int_{V} \frac{\partial N^{N}}{\partial x} \cdot k \cdot \frac{\partial θ}{\partial x} d V \\ - \int_{V} N^{N} r d V - \int_{S_{q}} N^{N} q d S = 0. \end{matrix} \end{matrix}

This nonlinear system is solved by a modified Newton method. The method is modified Newton because the tangent matrix (the Jacobian matrix)—that is, the rate of change of the left-hand side of Equation 6 with respect to $θ_{t + Δ t}^{N}$ —is not formed exactly. The formation of the terms in this tangent matrix is now described.

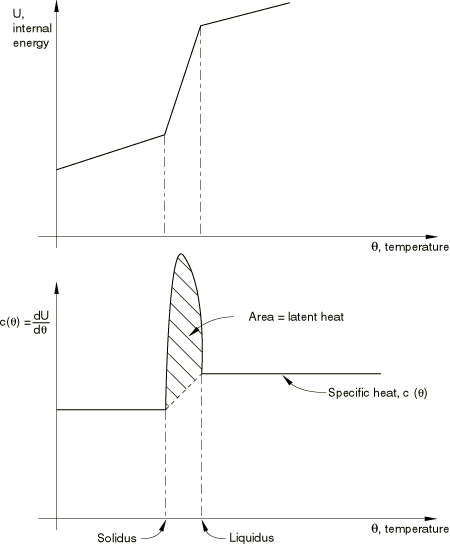
The internal energy term gives a Jacobian contribution:

\frac{1}{Δ t} \int_{V} N^{N} ρ \frac{d U}{d θ} |_{t + Δ t} N^{M} d V .

${(d U / d θ) |}_{t + Δ t}$ is the specific heat, $c (θ)$ , outside the latent heat range, and is $c + L / (θ_{L} - θ_{S})$ if $θ_{L} > θ_{t + Δ t} > θ_{S}$ at the integration point, where $θ_{L}$ and $θ_{S}$ are the liquidus and solidus temperatures and L is the latent heat associated with this phase change.

In severe latent heat cases this term can result in numerical instabilities, as the stiffness term $d U / d θ$ is small outside the solidus-liquidus temperature range and is very stiff inside that rather narrow range. To avoid such instabilities in those cases this term is modified to a secant term during the early iterations of the solution to a time step. Since the modification occurs only in cases involving latent heat, it affects only those problems.

The conductivity term gives a Jacobian contribution:

{\int_{V} \frac{\partial N^{N}}{\partial x} \cdot k |}_{t + Δ t} \cdot \frac{\partial N^{M}}{\partial x} d V + {{\int_{V} \frac{\partial N^{N}}{\partial x} \cdot \frac{\partial k}{\partial θ} |}_{t + Δ t} \cdot \frac{\partial θ}{\partial x} |}_{t + Δ t} N^{M} d V .

The second of these terms is typically small, since the conductivity usually varies only slowly with temperature. Because of this, and because the term is not symmetric, it is usually more efficient to omit it. This term is omitted unless the unsymmetric solver is chosen. Prescribed surface fluxes and body fluxes can also be temperature dependent and will then give rise to Jacobian contributions.

With film and radiation conditions, the surface flux term gives a Jacobian contribution:

{\int_{S} N^{N} \frac{\partial q}{\partial θ} |}_{t + Δ t} N^{M} d S .

For film conditions, $q = {}^{-}h (θ) (θ - θ^{o}),$

\frac{\partial q}{\partial θ} = - \frac{\partial h}{\partial θ} (θ - θ^{o}) - h,

while for radiation, $q = {}^{-}A (θ^{4} - θ^{o}^{4}),$

\frac{\partial q}{\partial θ} = {}^{-}4 A θ^{3} .

These terms are included in exactly this form in the Jacobian. The modified Newton method is then

\begin{matrix} (7) & \begin{matrix} {[\frac{1}{Δ t} \int_{V} N^{N} ρ \frac{d U}{d θ} |}_{t + Δ t} N^{M} d V & + {\int_{V} \frac{\partial N^{N}}{\partial x} \cdot k |}_{t + Δ t} \cdot \frac{\partial N^{M}}{\partial x} d V \\ + \int_{S} N^{N} (\frac{\partial h}{\partial θ} (θ - θ^{o}) + h + 4 A θ^{3}) N^{M} d S] \bar{c} ​^{M} \\ ​ = \int_{V} N^{N} r d V + \int_{S_{q}} N^{N} q d S - \frac{1}{Δ t} \int_{V} N^{N} ρ (U_{t + Δ t} - U_{t}) d V \\ - \int_{V} \frac{\partial N^{N}}{\partial x} \cdot k \cdot \frac{\partial θ}{\partial x} d V, \\ with θ_{t + Δ t, i + 1}^{N} & = θ_{t + Δ t, i}^{N} + {\bar{c}}^{N}, i = iteration
  number. \end{matrix} \end{matrix}

For purely linear systems Equation 7 is linear in ${\bar{c}}^{M}$ and, hence, in $θ_{t + Δ t}^{N}$ , so a single equation solution provides the $θ_{t + Δ t}^{N}$ . Since the method usually is only a minor modification of Newton's method, convergence is rapid.

Abaqus/Standard uses an automatic (self-adaptive) time stepping algorithm to choose $Δ t$ . This is based on a user-supplied tolerance on the maximum temperature change allowed in a time increment, and the increment is adjusted according to this parameter, as well as the convergence rate of Equation 7 in nonlinear cases.

The first-order heat transfer elements (such as 2-node link, 4-node quadrilateral, and 8-node brick) use a numerical integration rule with the integration stations located at the corners of the element for the heat capacitance terms. This means that the Jacobian term associated with the internal energy rate is diagonal. This approach is especially effective when strong latent heat effects are present. The second-order elements use conventional Gaussian integration. Thus, second-order elements are to be preferred for problems when the solution will be smooth (without latent heat effects), whereas the first-order elements should be used in nonsmooth cases (with latent heat).

The HEATCAP element is available for modeling lumped heat capacitance at a point. The associated concentrated film and concentrated radiation loading options are specified by the user. These loading options are also allowed in coupled temperature-displacement, coupled thermal-electrical, and coupled thermal-electrical-structural analyses.