Rebar modeling in two dimensions

ProductsAbaqus/StandardAbaqus/Explicit

Let $g_{i}, i = 1, 2$ be the element's usual isoparametric coordinates. Let r be an isoparametric coordinate along the line where the face of the element intersects the plane of reinforcement, with $- 1 \leq r \leq 1$ in an element (see Figure 1).

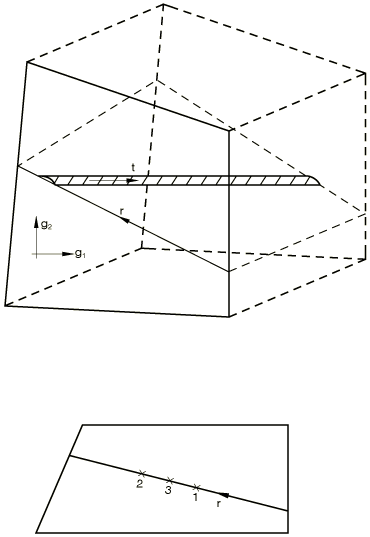
The plane of reinforcement is always perpendicular to the element face.

The rebar will be integrated at one or two points, depending on the order of interpolation in underlying elements. The volume of integration $(Δ V)$ , position, rebar strain $(ε)$ , and first and second variations of rebar strain $(δ ε$ and $d δ ε)$ at each point are calculated as

Δ V = \frac{A_{r}}{S_{r}} {(\frac{\partial x}{\partial r} \cdot \frac{\partial x}{\partial r})}^{\frac{1}{2}} t_{0} W_{N},

where

$t_{0}$: is the original thickness for plane elements and $2 π x_{1}$ for axisymmetric elements;
$A_{r}$: is the rebar cross-sectional area;
$S_{r}$: is the spacing of rebar (for axisymmetric elements $S_{r} = (x_{1} / x_{1}^{0}) S_{r}^{0}$ , where $x_{1}^{0}$ is the radius where the spacing $S_{r}^{0}$ is given);
$W_{N}$: is the Gauss weight associated with the integration point along the $(r)$ line;
$x = x (g_{i})$: is position; and

\frac{\partial x}{\partial r} = \frac{\partial x}{\partial g_{i}} \frac{\partial g_{i}}{\partial r} .

Strain is

ε = \frac{1}{2} \ln (\frac{d l^{2}}{d l_{o}^{2}}),

where $d l$ and $d l_{o}$ measure length along the rebar in the current and initial configurations, respectively.

For the deformations allowed in these elements,

{(\frac{d l}{d l_{o}})}^{2} = \cos^{2} α λ_{r}^{2} + \sin^{2} α λ_{t}^{2},

where $α$ is the orientation of the rebar from the plane of the model,

λ_{r}^{2} = \frac{\partial x}{\partial r} \cdot \frac{\partial x}{\partial r} / \frac{\partial x_{o}}{\partial r} \cdot \frac{\partial x_{o}}{\partial r}

is the squared stretch ratio in the r-direction, and $λ_{t}$ is the stretch ratio in the thickness direction:

$λ_{t} = 1$: for plane stress or plane strain;
$λ_{t} = t / t_{o}$: for generalized plane strain, where t is given in Generalized plane strain elements; and
$λ_{t} = x_{1} / x_{1_{o}}$: for axisymmetric elements.

From these results the first variation of strain is

δ ε = (\frac{d l_{o}}{d l})^{2} (\cos^{2} α \frac{\partial x}{\partial r} \cdot \frac{\partial δ x}{\partial r} / \frac{\partial x_{o}}{\partial r} \cdot \frac{\partial x_{o}}{\partial r} + δ p_{t}),

where

$δ p_{t} = 0$: for plane stress and plane strain,
$δ p_{t} = \sin^{2} α t δ t / t_{o}^{2}$: for generalized plane strain, and
$δ p_{t} = \sin^{2} α x_{1} δ x_{1} / x_{1_{o}}^{2}$: for axisymmetric cases.

The second variation of strain is then

\begin{matrix} d δ ε & ​ = - 2 {(\frac{d l_{o}}{d l})}^{2} (\cos^{2} α \frac{\partial x}{\partial r} \cdot \frac{\partial δ x}{\partial r} / \frac{\partial x_{o}}{\partial r} \cdot \frac{\partial x_{o}}{\partial r} + δ p_{t}) \\ ​ \cdot (\cos^{2} α \frac{\partial x}{\partial r} \cdot \frac{\partial d x}{\partial r} / \frac{\partial x_{o}}{\partial r} \cdot \frac{\partial x_{o}}{\partial r} + d p_{t}) \\ + {(\frac{d l_{o}}{d l})}^{2} (\cos^{2} α \frac{\partial d x}{\partial r} \cdot \frac{\partial δ x}{\partial r} / \frac{\partial x_{o}}{\partial r} \cdot \frac{\partial x_{o}}{\partial r} + d δ p_{t}) . \end{matrix}