J-integral evaluation

In the context of quasi-static analysis the J-integral is defined in two dimensions as

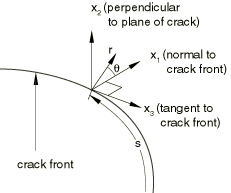
where $\mathrm{\Gamma }$ is a contour beginning on the bottom crack surface and ending on the top surface, as shown in Figure 1; the limit $\mathrm{\Gamma }\to 0$ indicates that $\mathrm{\Gamma }$ shrinks onto the crack tip; $\mathbf{q}$ is a unit vector in the virtual crack extension direction; and $\mathbf{n}$ is the outward normal to $\mathrm{\Gamma }$. $\mathbf{H}$ is given by

For elastic material behavior W is the elastic strain energy; for elastic-plastic or elastic-viscoplastic material behavior W is defined as the elastic strain energy density plus the plastic dissipation, thus representing the strain energy in an “equivalent elastic material.” This implies that the J-integral calculation is suitable only for monotonic loading of elastic-plastic materials.

Figure 1. Contour for evaluation of the J-integral.

Following Shih et al. (1986), we rewrite Equation 1 in the form

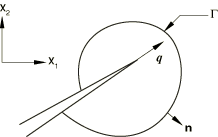
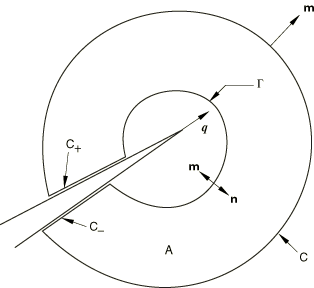
where $\overline{\mathbf{q}}$ is a sufficiently smooth weighting function within the region enclosed by the closed contour $C+C_{+}+\mathrm{\Gamma }+C_{-}$ and has the value $\overline{\mathbf{q}}=\mathbf{q}$ on $\mathrm{\Gamma }$ and $\overline{\mathbf{q}}=0$ on C; and $\mathbf{m}$ is the outward normal to the domain enclosed by the closed contour, as shown in Figure 2. $\mathbf{m}=-\mathbf{n}$ on $\mathrm{\Gamma }$; and $\mathbf{t}=\mathbf{m}\cdot \mathit{\sigma }$ is the surface traction on the crack surfaces $C_{+}$ and $C_{-}$.

Figure 2. Closed contour $C+C_{+}+\mathrm{\Gamma }+C_{-}$ encloses a domain A that includes the crack-tip region as $\mathrm{\Gamma }\to 0.$

Using the divergence theorem, we convert the closed contour integral into the domain integral

where A is the domain enclosed by the closed contour $C+C_{+}+\mathrm{\Gamma }+C_{-}$. It is worth noting that the domain A includes the crack-tip region as $\mathrm{\Gamma }\to 0$.

If equilibrium is satisfied and W is a function of the mechanical strain—i.e., $W=W\left({\mathit{\epsilon }}^m\right)$—we have

where $\mathbf{f}$ is the body force per unit volume and ${\mathit{\epsilon }}^{th}$ is the thermal strain. Substituting the above two equations into Equation 3 gives

To evaluate these integrals, Abaqus defines the domain in terms of rings of elements surrounding the crack tip. Different “contours” (domains) are created. The first contour consists of those elements directly connected to crack-tip nodes. The next contour consists of the ring of elements that share nodes with the elements in the first contour as well as the elements in the first contour. Each subsequent contour is defined by adding the next ring of elements that share nodes with the elements in the previous contour. $\overline{\mathbf{q}}$ is chosen to have a magnitude of zero at the nodes on the outside of the contour and to be one (in the crack direction) at all nodes inside the contour except for the midside nodes (if they exist) in the outer ring of elements. These midside nodes are assigned a value between zero and one according to the position of the node on the side of the element.

The J-integral can be extended to three dimensions by considering a crack with a tangentially continuous front, as shown in Figure 3. The local direction of virtual crack extension is again given by $\mathbf{q}$,

Figure 3. Definition of local orthogonal Cartesian coordinates at the point s on the crack front; the crack is in the $x_1$–$x_3$ plane.

which is perpendicular to the local crack front and lies in the crack plane. Asymptotically, as $r\to 0$, the conditions for path independence apply on any contour in the $x_1$–$x_2$ plane, which is perpendicular to the crack front at s. Hence, the J-integral defined in this plane can be extended to represent the pointwise energy release rate along the crack front as

For a virtual crack advance $\lambda \left(s\right)$ in the plane of a three-dimensional crack, the energy release rate is given by

where L denotes the crack front under consideration; $dA$ is a surface element on a vanishingly small tubular surface enclosing the crack tip (i.e., $dA=dsd\mathrm{\Gamma }$); and $\mathbf{n}$ is the outward normal to $dA$. $\overline{J}$ can be calculated by the domain integral method similar to that used in two dimensions. To do so, we first convert the surface integral in Equation 6 to a volume integral by introducing a contour surface $A_o$, outside surface $A_t$, external surfaces $A_{ends}$ at the ends of the crack front (the surfaces $A_{ends}$ vanish for the crack whose front forms a closed loop), and the crack faces $A_{cracks}$, as shown in Figure 4.

Figure 4. Surface $A=A_t+A_o+A_{ends}+A_{cracks}$ encloses a domain volume V that includes the crack-front region as $\mathrm{\Gamma }\to 0.$

It can be seen that $A=A_t+A_o+A_{ends}+A_{cracks}$ encloses a volume V. A weighting function $\overline{\mathbf{q}}$ is defined such that it has a magnitude of zero on $A_o$ and $\overline{\mathbf{q}}=\lambda \left(s\right)\mathbf{q}$ on $A_t$. $\overline{\mathbf{q}}$ is assumed to vary smoothly between these values within A. On the external surfaces $A_{ends}$ where $\mathbf{q}$ is not tangential to the surfaces, it must be made so. This can be done in Abaqus by defining the surface normals explicitly. Then, we can rewrite Equation 6 as

where $\mathbf{m}$ is the outward normal to A (and $\mathbf{m}=-\mathbf{n}$ on $A_t$). $\mathbf{t}=\mathbf{m}\cdot \mathit{\sigma }$ is the surface traction on surfaces $A_{ends}$ and the crack surfaces $A_{cracks}$.

Using the divergence theorem, we obtain

To obtain $J\left(s\right)$ at each node set P along the crack front line, $\lambda \left(s\right)$ is discretized with the same interpolation functions as those used in the finite elements along the crack front:

where ${\lambda }^Q=1$ at the node set P and all other ${\lambda }^Q$ are zero. This expression for $\lambda \left(s\right)$ is substituted into Equation 8. Finally, the J-integral value at each node set P along the crack front can be calculated as