Mohr-Coulomb Plasticity

The Mohr-Coulomb criterion assumes that yield occurs when the shear stress on any point in a material reaches a value that depends linearly on the normal stress in the same plane. The Mohr-Coulomb model is based on plotting Mohr's circle for states of stress at yield in the plane of the maximum and minimum principal stresses. The yield line is the best straight line that touches these Mohr's circles (Figure 1).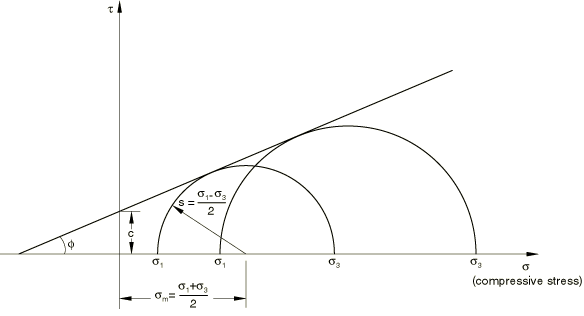

Figure 1. Mohr-Coulomb yield model.

Therefore, the Mohr-Coulomb model is defined by

where $\sigma$ is negative in compression. From Mohr's circle,

Substituting for $\tau$ and $\sigma$, multiplying both sides by $\cos \varphi$, and reducing, the Mohr-Coulomb model can be written as

where

is half of the difference between the maximum principal stress, ${\sigma }_1$, and the minimum principal stress, ${\sigma }_3$ (and is, therefore, the maximum shear stress),

is the average of the maximum and minimum principal stresses, and $\varphi$ is the friction angle.

For general states of stress the model is more conveniently written in terms of three stress invariants as

where

$\varphi$

is the slope of the Mohr-Coulomb yield surface in the p–$R_{mc}q$ stress plane (see Figure 2), which is commonly referred to as the friction angle of the material and can depend on temperature and predefined field variables;

c

is the cohesion of the material; and

$\mathrm{\Theta }$

is the deviatoric polar angle defined as

$$\cos \left(3\mathrm{\Theta }\right)={\left(\frac{r}{q}\right)}^3,$$

and

$p=-\frac{1}{3}\mathrm{trace}\left(\mathit{\sigma }\right)$

is the equivalent pressure stress,

$q=\sqrt{\frac{3}{2}(\mathbf{S}:\mathbf{S})}$

is the Mises equivalent stress,

$r={(\frac{9}{2}\mathbf{S}\cdot \mathbf{S}:\mathbf{S})}^{\frac{1}{3}}$

is the third invariant of deviatoric stress, and

$\mathbf{S}=\mathit{\sigma }+p\mathbf{I}$

is the deviatoric stress.

The friction angle, $\varphi$, controls the shape of the yield surface in the deviatoric plane as shown in Figure 2. The tension cutoff surface is shown for a meridional angle of $\mathrm{\Theta }=0$. The friction angle range is $0^{\circ }\le \varphi <{90}^{\circ }$. In the case of $\varphi =0^{\circ }$ the Mohr-Coulomb model reduces to the pressure-independent Tresca model with a perfectly hexagonal deviatoric section. In the case of $\varphi ={90}^{\circ }$ the Mohr-Coulomb model reduces to the “tension cutoff” Rankine model with a triangular deviatoric section and $R_{mc}=\mathrm{\infty }$ (this limiting case is not permitted within the Mohr-Coulomb model described here).

When using one-element tests to verify the calibration of the model, the output variables SP1, SP2, and SP3 correspond to the principal stresses ${\sigma }_3$, ${\sigma }_2$, and ${\sigma }_1$, respectively.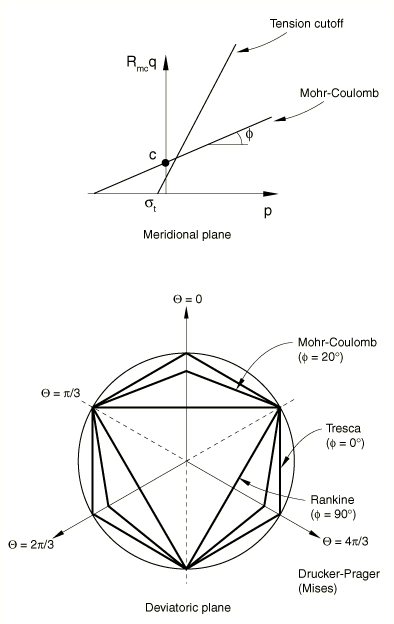

Figure 2. Mohr-Coulomb and tension cutoff surfaces in meridional and deviatoric planes.

Isotropic cohesion hardening is assumed for the hardening behavior of the Mohr-Coulomb yield surface. The hardening curve must describe the cohesion yield stress as a function of plastic strain and, possibly, temperature and predefined field variables. In defining this dependence at finite strains, “true” (Cauchy) stress and logarithmic strain values should be given. An optional tension cutoff hardening (or softening) curve can be specified

Rate dependency effects are not accounted for in this plasticity model.

            
              MOHR COULOMB
            
            
          

            
              MOHR COULOMB HARDENING
            
            
          

Property module: material editor: MechanicalPlasticityMohr Coulomb Plasticity

Property module: material editor: MechanicalPlasticityMohr Coulomb Plasticity: Cohesion

In Abaqus tension cutoff is modeled using the Rankine surface, which is written as

where $R_r\left(\mathrm{\Theta }\right)=\left(2/3\right)\cos \mathrm{\Theta }$, and ${\sigma }_t$ is the tension cutoff value representing softening (or hardening) of the Rankine surface, as a function of tensile equivalent plastic strain, ${\overline{{\epsilon }_t}}^{pl}$.

            
              TENSION CUTOFF
            
            
          

Property module: material editor: MechanicalPlasticityMohr Coulomb Plasticity: toggle on Specify tension cutoff; Tension Cutoff

The flow potential, G, for the Mohr-Coulomb yield surface is chosen as a hyperbolic function in the meridional stress plane and the smooth elliptic function proposed by Menétrey and Willam (1995) in the deviatoric stress plane:

where

and

$\psi$

is the dilation angle measured in the p–$R_{mw}q$ plane at high confining pressure and can depend on temperature and predefined field variables;

${c|}_0$

is the initial cohesion yield stress, ${c|}_0={c|}_{{\overline{\epsilon }}^{pl}=0}$;

$\mathrm{\Theta }$

is the deviatoric polar angle defined previously;

$ϵ$

is a parameter, referred to as the meridional eccentricity, that defines the rate at which the hyperbolic function approaches the asymptote (the flow potential tends to a straight line in the meridional stress plane as the meridional eccentricity tends to zero); and

e

is a parameter, referred to as the deviatoric eccentricity, that describes the “out-of-roundedness” of the deviatoric section in terms of the ratio between the shear stress along the extension meridian ($\mathrm{\Theta }=0$) and the shear stress along the compression meridian ($\mathrm{\Theta }=\frac{\pi }{3}$).

A default value of $0.1$ is provided for the meridional eccentricity, $ϵ$.

By default, the deviatoric eccentricity, e, is calculated as

where $\varphi$ is the Mohr-Coulomb friction angle; this calculation corresponds to matching the flow potential to the yield surface in both triaxial tension and compression in the deviatoric plane. Alternatively, Abaqus allows you to consider this deviatoric eccentricity as an independent material parameter; in this case you provide its value directly. Convexity and smoothness of the elliptic function requires that $1/2<e\le 1$. The upper limit, $e=1$ (or $\varphi =$ 0° when you do not specify the value of e), leads to $R_{mw}(\mathrm{\Theta },e=1)=R_{mc}(\frac{\pi }{3},\varphi )$, which describes the Mises circle in the deviatoric plane. The lower limit, $e=1/2$ (or $\varphi =$ 90° when you do not specify the value of e), leads to $R_{mw}(\mathrm{\Theta },e=1/2)=2R_{mc}(\frac{\pi }{3},\varphi )\cos \mathrm{\Theta }$ and would describe the Rankine triangle in the deviatoric plane (this limiting case is not permitted within the Mohr-Coulomb model described here).

This flow potential, which is continuous and smooth, ensures that the flow direction is always uniquely defined. A family of hyperbolic potentials in the meridional stress plane is shown in Figure 3, and the flow potential in the deviatoric stress plane is shown in Figure 4.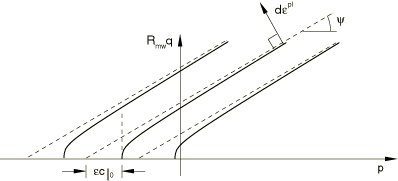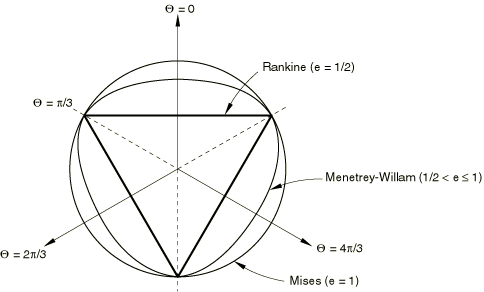

Figure 3. Family of hyperbolic flow potentials in the meridional stress plane.

Figure 4. Menétrey-Willam flow potential in the deviatoric stress plane.

Flow in the meridional stress plane can be close to associated when the angle of friction, $\varphi$, and the angle of dilation, $\psi$, are equal and the meridional eccentricity, $ϵ$, is very small; however, flow in this plane is, in general, nonassociated. Flow in the deviatoric stress plane is always nonassociated.

            
              MOHR COULOMB
            
            
          

MOHR COULOMB, DEVIATORIC ECCENTRICITY=e

Property module: material editor: MechanicalPlasticityMohr Coulomb Plasticity: Plasticity: Deviatoric eccentricity: Calculated default

Property module: material editor: MechanicalPlasticityMohr Coulomb Plasticity: Plasticity: Deviatoric eccentricity: Specify: e

A flow potential that results in a nearly associative flow is chosen for the Rankine surface and is constructed by modifying the Menétrey-Willam potential described earlier:

where

${{\sigma }_t|}_0$

is the initial value of tension cutoff;

${ϵ}_t$

is the meridional eccentricity, similar to $ϵ$ defined earlier; and

$e_t$

is the deviatoric eccentricity, similar to $e$ defined earlier.

Abaqus uses values of $0.1$ and $0.6$, for ${ϵ}_t$ and $e_t$, respectively.

Since the plastic flow is nonassociated in general, the use of this Mohr-Coulomb model generally requires the unsymmetric matrix storage and solution scheme in Abaqus/Standard (see Defining an Analysis).