*MATRIX ASSEMBLE

Define stiffness, mass, or damping matrices for a part of the model.

This option can be used to identify a stiffness, mass, or damping matrix that will be assembled into the corresponding global finite element matrix. This matrix must have been input previously by using the MATRIX INPUT option. The option also unites all the matrices from the same original model and allows you to remap their user nodes to new labels. Matrices from different original models must be specified by repeating the MATRIX ASSEMBLE option.

Positioning transformations are applied in the order in which they are specified. Translation, rotation, and reflection transformations are supported. There is no restriction on the number of translations, rotations, and reflections that you can apply in a single MATRIX ASSEMBLE option.

This page discusses:

See Also
*MATRIX INPUT
In Other Guides
Using Matrices

ProductsAbaqus/Standard

TypeModel data

LevelModel

At least one of the following parameters is required

MASS

Set this parameter equal to the name of the mass matrix.

STIFFNESS

Set this parameter equal to the name of the stiffness matrix.

STRUCTURAL DAMPING

Set this parameter equal to the name of the structural damping matrix.

VISCOUS DAMPING

Set this parameter equal to the name of the viscous damping matrix.

Optional parameters

NAME

This parameter specifies a matrix subassembly name.

If this parameter is omitted, a default name is assigned to each subassembly: Assemble-1, Assemble-2, etc.

NSET

This parameter remaps nodes of the assembled matrices at the usage level. Set this parameter equal to the name of the node set that contains the new node labels corresponding to the matrix nodes. You can map all user-defined nodes of the matrices or the interface nodes only, if defined. The size of the node set and the order of the nodes in the set must fully correspond to the combined set of nodes of all the matrices for all nodes or only interface nodes. If necessary, use an unsorted node set to obtain the correct mapping. The default matrix nodes order is in ascending order of their original labels defined at generation or specified in the matrix data.

If this parameter is omitted, all user-defined nodes retain their original labels.

POSITION TOL
Set this parameter equal to the tolerance on the distance between usage level nodes and the corresponding matrix nodes. If this parameter is omitted, the default is a tolerance of 10–4 times the largest estimated characteristic dimension within the matrix subassembly. If the parameter is given with a value of 0.0, the position of the matrix nodes is not checked.

Data lines to translate a matrix subassembly

First line
  1. TRANSLATE (transformation type).

  2. Value of the translation to be applied in the global X-direction.

  3. Value of the translation to be applied in the global Y-direction.

  4. Value of the translation to be applied in the global Z-direction.

Repeat this data line as often as necessary to define matrix subassembly translations.

Data lines to rotate a matrix subassembly

First line
  1. ROTATE (transformation type).
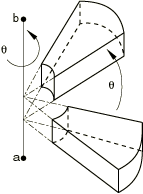
  2. Global X-coordinate of point a on the axis of rotation (see Figure 1).
  3. Global Y-coordinate of point a on the axis of rotation.
  4. Global Z-coordinate of point a on the axis of rotation.
  5. Global X-coordinate of point b on the axis of rotation.
  6. Global Y-coordinate of point b on the axis of rotation.
  7. Global Z-coordinate of point b on the axis of rotation.
  8. Angle of rotation about the a–b axis (in degrees).

Repeat this data line as often as necessary to define matrix subassembly rotations.

Data lines to reflect a matrix subassembly

First line
  1. REFLECT (transformation type).
  2. Global X-coordinate of point a in the plane of reflection (see Figure 2).
  3. Global Y-coordinate of point a in the plane of reflection.
  4. Global Z-coordinate of point a in the plane of reflection.
  5. Global X-coordinate of point b in the plane of reflection.
  6. Global Y-coordinate of point b in the plane of reflection.
  7. Global Z-coordinate of point b in the plane of reflection.
  8. Global X-coordinate of point c in the plane of reflection.
  9. Global Y-coordinate of point c in the plane of reflection.
  10. Global Z-coordinate of point c in the plane of reflection.

Repeat this data line as often as necessary to define matrix subassembly reflections.

Data lines to reflect a matrix subassembly using the Euler angles ϕ, θ, and ψ

First line
  1. EULER (transformation type).
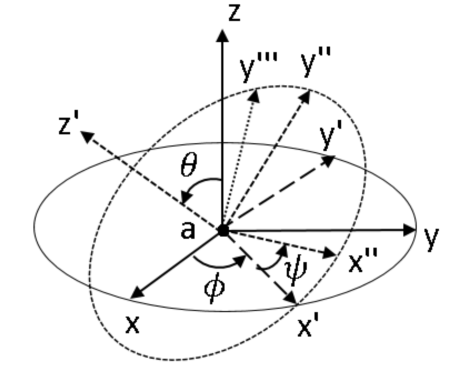
  2. Precession angle, ϕ, of rotation about the z-axis (in degrees) (see Figure 3).
  3. Nutation angle, θ, of rotation about the x′-axis (in degrees).
  4. Intrinsic rotation angle, ψ, of rotation about the z′-axis (in degrees).
  5. Global X-coordinate of the reference point, O (optional; default value is zero).
  6. Global Y-coordinate of the reference point, O (optional; default value is zero).
  7. Global Z-coordinate of the reference point, O (optional; default value is zero).

Repeat this data line as often as necessary to define matrix subassembly reflections using the Euler angles.

Figure 1. Matrix subassembly rotation.

Figure 2. Matrix subassembly reflection. Points a, b, and c cannot be collinear.

Figure 3. Euler angles.