Techniques for reducing volumetric locking

A small amount of compressibility is introduced into the rubber material model in order to alleviate volumetric locking. Provided the amount of compressibility is small, the results obtained with a nearly incompressible material will be very similar to those obtained with an incompressible material.

Compressibility is introduced by setting the material constant D1 to a nonzero value. The value is chosen so that the initial Poisson's ratio, ν0, is close to 0.5. The equations given in Hyperelastic Behavior of Rubberlike Materials can be used to relate D1 and ν0 in terms of μ0 and K0 (the initial shear and bulk moduli, respectively) for the polynomial form of the strain energy potential. For example, the hyperelastic material coefficients obtained earlier from the test data (see The hyperelastic material parameters in Preprocessing—creating the model with Abaqus/CAE) were given as C10=​ 176051 and C01=​ 4332.63; thus, setting D1=​ 5.E−7 yields ν0=​ 0.46.

A model incorporating compressibility with additional mesh refinement (to reduce mesh distortion) is shown in Figure 1 (this mesh can be generated easily by changing the edge seeds in Abaqus/CAE or another preprocessor).

Figure 1. Modified mesh with refinement at both corners.

The deformed shape associated with this model is shown in Figure 2.

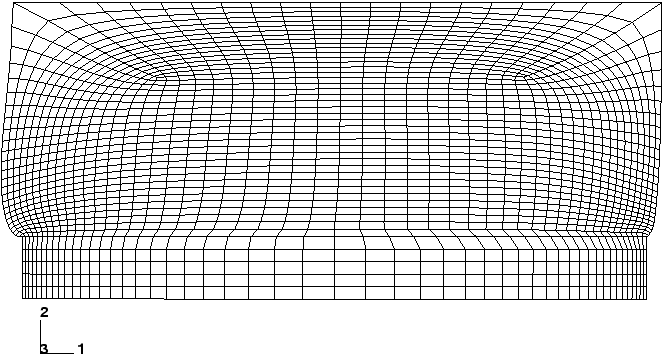
Figure 2. Deformed shape of the modified mesh.

It is clear from this figure that the mesh distortion has been reduced significantly in the critical regions of the rubber model. Examining contour plots of the pressure (without averaging across elements) reveals a smooth variation in pressure stress between elements. Thus, volumetric locking has been eliminated.