Steady-state rolling analysis of a tire

A description of the tire and finite element model is given in Symmetric results transfer for a static tire analysis. To take into account the effect of the skew symmetry of the actual tire in the dynamic analysis, the steady-state rolling analysis is performed on the full three-dimensional model, also referred to as the full model. Inertia effects are ignored since the rolling speed is low ($v_0=$ 10 km/h).

As stated earlier, the steady-state transport capability in Abaqus uses a mixed Eulerian/Lagrangian approach in which, to an observer in the moving reference frame, the material appears to flow through a stationary mesh. The paths that the material points follow through the mesh are referred to as streamlines and must be computed before a steady-state transport analysis can be performed. As discussed in Symmetric results transfer for a static tire analysis, the streamlines needed for the steady-state transport analyses in this example are computed using the revolve functionality for symmetric model generation.

The incompressible hyperelastic material used to model the rubber in this example includes a time-domain viscoelastic component, which is specified directly using the Prony series parameters. A simple 1-term Prony series model is used. For an incompressible material a 1-term Prony series in Abaqus is defined by providing a single value for the shear relaxation modulus ratio, ${\overline{g}}_1^P$, and its associated relaxation time, ${\tau }_1$. In this example ${\overline{g}}_1^P$ = 0.3 and ${\tau }_1$ = 0.1. The viscoelastic—i.e., material history—effects are included in a steady-state transport step unless you are investigating the long-term behavior of the material. See Time Domain Viscoelasticity for a more detailed discussion of modeling time-domain viscoelasticity in Abaqus.

As discussed in Symmetric results transfer for a static tire analysis, it is recommended that the footprint analyses be obtained with a friction coefficient of zero (so that no frictional forces are transmitted across the contact surface). The frictional stresses for a rolling tire are very different from the frictional stresses in a stationary tire, even if the tire is rolling at very low speed; therefore, discontinuities may arise in the solution between the last static analysis and the first steady-state transport analysis. Furthermore, varying the friction coefficient from zero at the beginning of the steady-state transport step to its final value at the end of the steady-state transport step ensures that the changes in frictional forces reduce with smaller load increments. This is important if Abaqus must take a smaller load increment to overcome convergence difficulties while trying to obtain the steady-state rolling solution.

Once the static footprint solution for the tire has been computed, the steady-state rolling contact problem can be solved using steady-state transport. The objective of the first simulation in this example is to obtain the straight line, steady-state rolling solutions, including full braking and full traction, at different spinning velocities. We also compute the straight line, free rolling solution. In the second simulation free rolling solutions at different slip angles are computed. In the first and second simulations material history effects are ignored by specifying that the long-term behavior of the material is to be used. The third simulation repeats a portion of the straight line, steady-state rolling analysis from the first simulation; however, material history effects are included if you do not specify a long-term material response. A steady ground velocity of 10.0 km/h is maintained for all the simulations. The objective of the fourth simulation is to obtain the free rolling solution of the tire in contact with a 1.5 m rigid drum rotating at 3.7 rad/s.

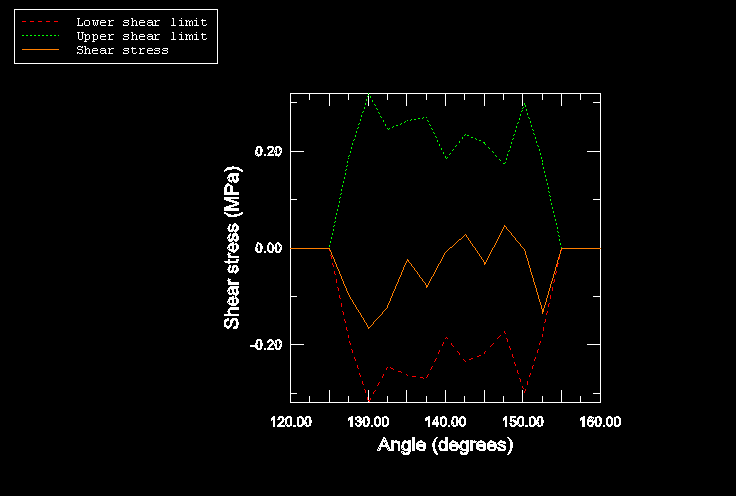
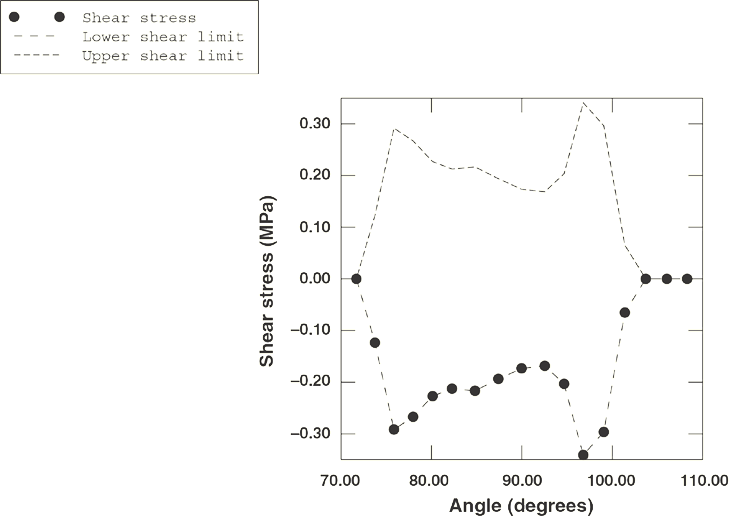
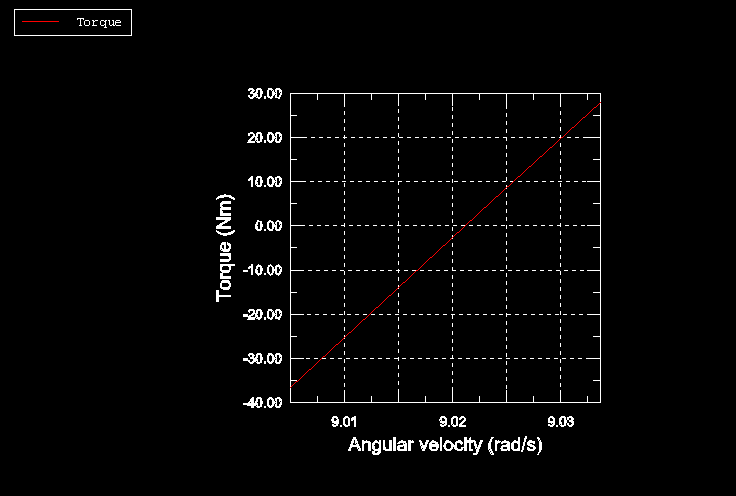
In the first simulation (rollingtire_brake_trac.inp) the full braking solution is obtained in the first steady-state transport step by setting the friction coefficient, $\mu$, to its final value of 1.0 by changing friction properties and applying the translational ground velocity together with a spinning angular velocity that will result in full braking. An estimate of the angular velocity corresponding to full braking is obtained as follows. A free rolling tire generally travels farther in one revolution than determined by its center height, H, but less than determined by the free tire radius. In this example the free radius is 316.2 mm and the vertical deflection is approximately 20.0 mm, so $H=$ 296.2 mm. Using the free radius and the effective height, it is estimated that free rolling occurs at an angular velocity between $\omega =$ 8.78 rad/s and $\omega =$ 9.38 rad/s. Smaller angular velocities would result in braking, and larger angular velocities would result in traction. We use an angular velocity $\omega =$ 8.0 rad/s to ensure that the solution in the first steady-state transport step is a full braking solution (all contact points are slipping, so the magnitude of the total frictional force across the contact surface is $\mu N$).

In the second steady-state transport analysis step of the full model, the angular velocity is increased gradually to $\omega =$ 10.0 rad/s while the ground velocity is held constant. The solution at each load increment is a steady-state solution to the loads acting on the structure at that instant so that a series of steady-state solutions between full braking and full traction is obtained. This analysis provides us with a preliminary estimate of the free rolling velocity. The second simulation (rollingtire_trac_res.inp) performs a refined search around the first estimate of free rolling conditions.

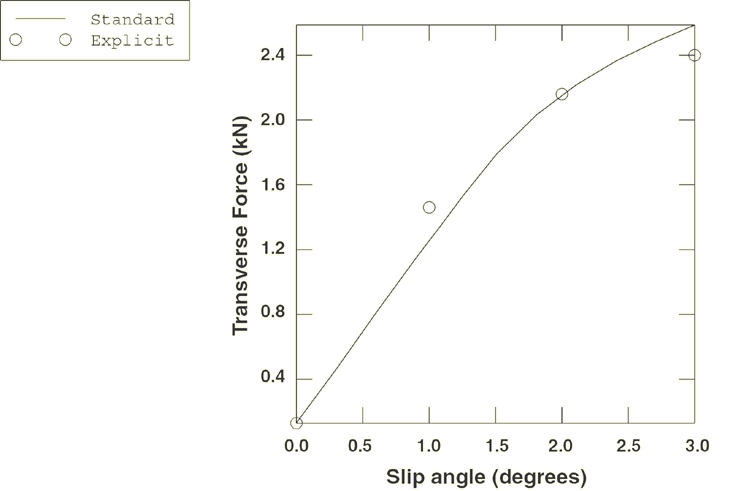
In the third simulation (rollingtire_slipangles.inp) the free rolling solutions at different slip angles are computed. The slip angle, $\theta$, is the angle between the direction of travel and the plane normal to the axle of the tire. In the first step the straight line, free rolling solution from the first simulation is brought into equilibrium. This step is followed by a steady-state transport step where the slip angle is gradually increased from $\theta =$ 0.0° at the beginning of the step to $\theta =$ 3.0° at the end of the step, so a series of steady-state solutions at different slip angles is obtained. This is accomplished by prescribing a traveling velocity vector with components $v_x=v_0\cos \theta$ and $v_y=v_0\sin \theta$ in the prescribed translational motion, where $\theta =$ 0.0° in the first steady-state transport step and $\theta =$ 3.0° at the end of the second steady-state transport step.

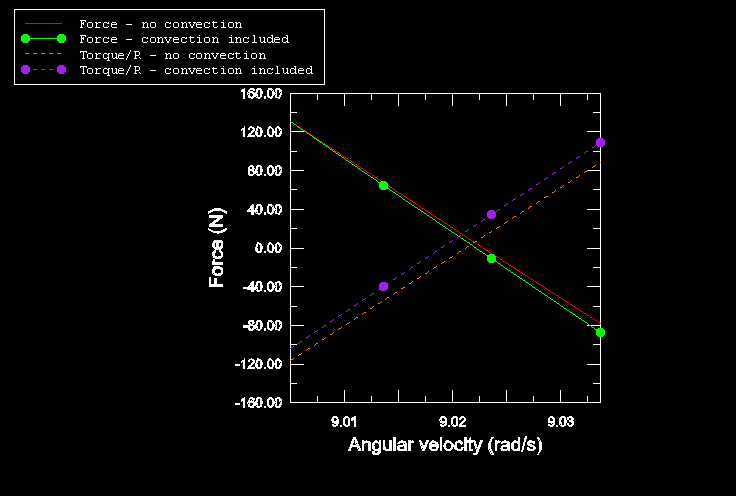
The fourth simulation (rollingtire_materialhistory.inp) includes a series of steady-state solutions between full braking and full traction in which the material history effects are included.

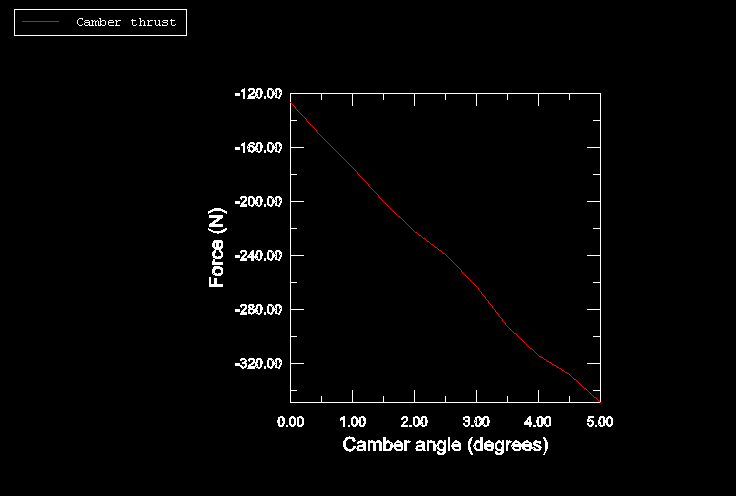
The fifth simulation (rollingtire_camber.inp) analyzes the effect of camber angle on the lateral thrust at the contact patch under free rolling conditions.

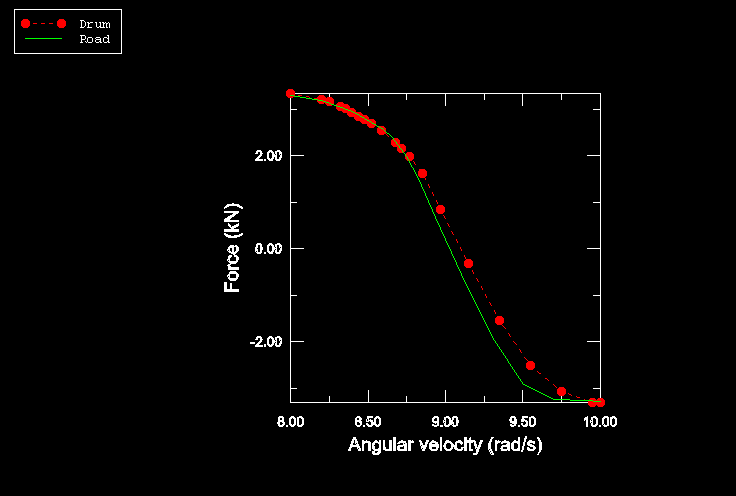
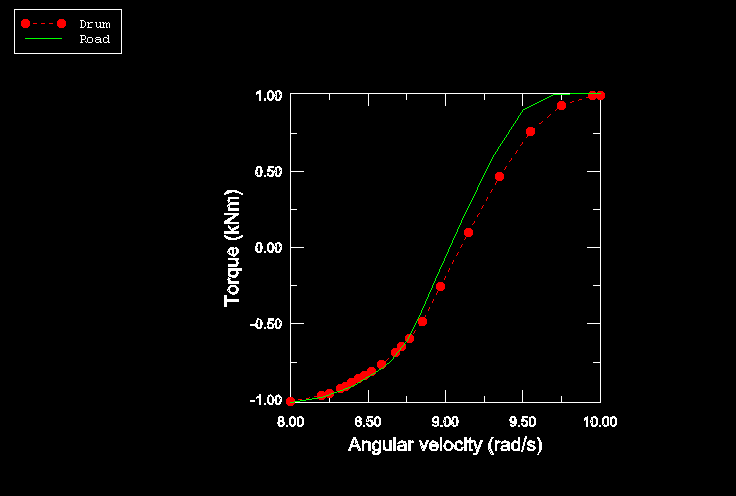
The final simulation in this example (rollingtire_drum.inp) considers a tire in contact with a rigid rotating drum. The loading sequence is similar to the loading sequence used in the first simulation. However, in this simulation the translational velocity of the tire is zero, and a rotational angular velocity is applied to the reference node of the rigid drum. Since a prescribed load is applied to the rigid drum reference node to establish contact between the tire and drum, the rotation axis of the drum is unknown prior to the analysis. Abaqus automatically updates the rotation axis to its current position if the angular velocity is defined. The rotational velocity of the rigid surface can also be defined. In that case the position and orientation of the axis of revolution must be defined in the steady-state configuration and, therefore, must be known prior to the analysis. The position and orientation of the axis are applied at the beginning of the step and remain fixed during the step. When the drum radius is large compared to the axle displacement, as in this example, it is a reasonable approximation to define the axle in the original configuration without significantly affecting the accuracy of the results.

SIMULIA gratefully acknowledges Hankook Tire and Yokohama Rubber Company for their cooperation in developing the steady-state transport capability used in this example. SIMULIA thanks Dr. Koishi of Yokohama Rubber Company for supplying the geometry and material properties used in this example.