Hydrostatic fluid elements: modeling an airspring

This section shows two examples of the analysis of a cord-reinforced rubber airspring. Static analyses are performed in Abaqus/Standard, and quasi-static analyses are performed in Abaqus/Explicit.

This page discusses:

Geometry and model
Symmetry boundary conditions and initial shell curvature
Material properties
Loading
Results and discussion
Input files
References
Figures

Products Abaqus/Standard Abaqus/Explicit

Airsprings are rubber or fabric actuators that support and contain a column of compressed air. They are used as pneumatic actuators and vibration isolators. Unlike conventional pneumatic cylinders, airsprings have no pistons, rods, or dynamic seals. This makes them better suited to handle off-center loading and shock. In addition, airsprings are considerably more flexible than other types of isolators: the airspring's inflation pressure can be changed to compensate for different loads or heights without compromising isolation efficiency. Dils (1992) provides a brief discussion of various practical uses of airsprings.

The first example is a three-dimensional, half-symmetry model that uses finite-strain shell elements to model the rubber spring and rebar to model the multi-ply steel reinforcements in the rubber membrane. In addition, a three-dimensional, element-based rigid surface is used to define the contact between the airspring and the lateral metal bead. The cord-reinforced rubber membrane is modeled using a hyperelastic material model with steel rebar.

The second example is a two-dimensional, axisymmetric version of the first model that uses composite axisymmetric, finite-strain shell elements to model the cord-reinforced rubber spring and an axisymmetric, element-based rigid surface in the contact definition. This model uses a composite shell section consisting of a thin orthotropic elastic layer sandwiched between two hyperelastic layers. The orthotropic layer captures the mechanical properties of the rebar definition used in the three-dimensional model.

The orthotropic material constants have been obtained by performing simple tests on a typical element of the three-dimensional model. The three-dimensional shell model uses rebar with material properties that are initially identical to the properties of the composite shell section in the axisymmetric shell model.

For comparison, Abaqus/Standard input files that use finite-strain membrane elements instead of finite-strain shell elements to model the cord-reinforced rubber spring are also included for both the axisymmetric and three-dimensional models.

In all analyses the airspring cavity is modeled using the surface-based fluid cavity capability (see About Surface-Based Fluid Cavities) and air inside the cavity is modeled as a compressible or “pneumatic” fluid satisfying the ideal gas law.

Geometry and model

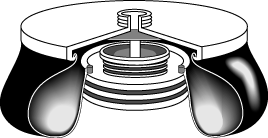
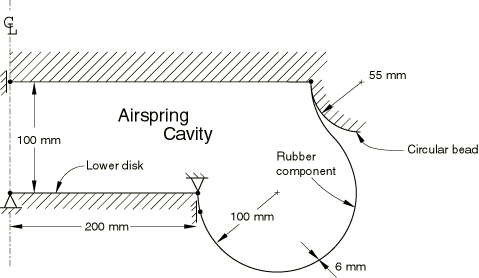
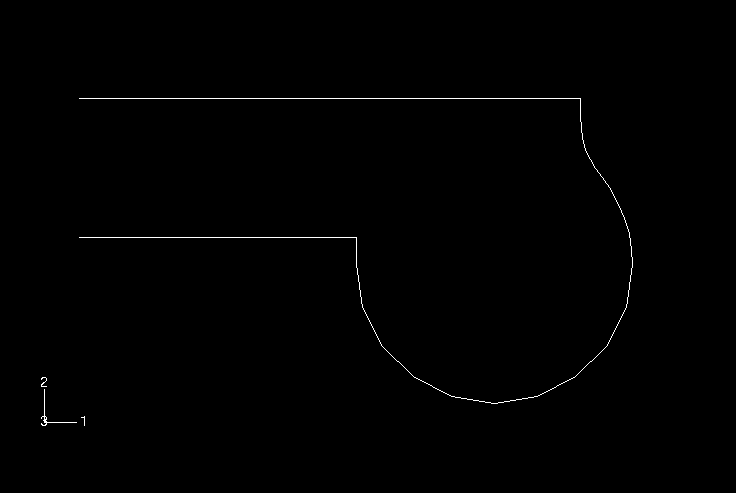
The dimensions of the airspring have been inferred from the paper by Fursdon (1990). This airspring, shown in Figure 1, is fairly large and is used in secondary suspension systems on railway bogies. However, the shape of the airspring is typical of airsprings used in other applications. The airspring's cross-section is shown in Figure 2. The airspring is toroidal in shape, with an inner radius of 200 mm and an outer radius of 400 mm. The airspring has been idealized in the model as consisting of two circular, metal disks connected to each other via a rubber component. The lower disk has a radius of 200 mm, and the upper disk has a radius of 362.11 mm. The disks are initially coaxial and are 100 mm apart. The rubber component is doubly curved and toroidal in shape. The rubber is constrained in the radial direction by a circular bead 55 mm in radius that goes around the circumference of the upper disk.

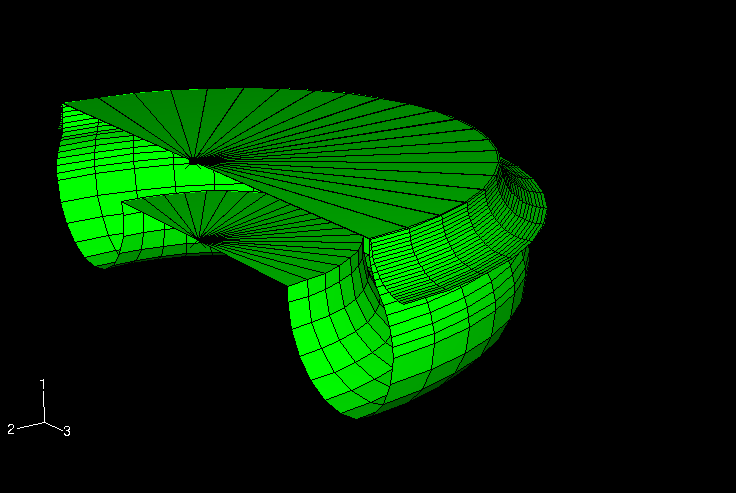
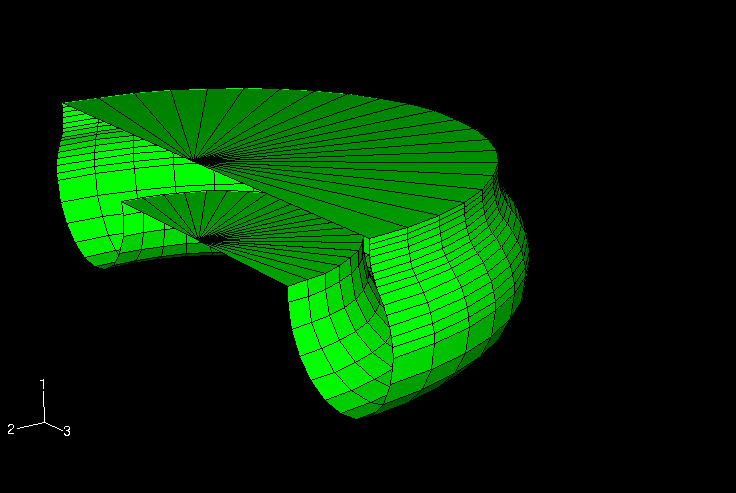
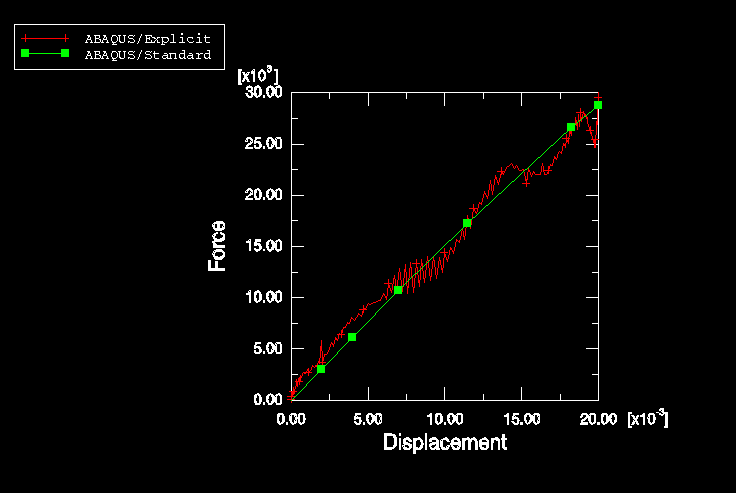
The rubber “hose” in the half-symmetry, three-dimensional model is modeled with 550 S4R finite-strain shell elements. The mesh in the upper hemisphere of the hose is more refined than that in the lower hemisphere, because the rubber membrane undergoes a reversal in curvature in the upper region as it contours the circular bead attached to the upper disk. The circular bead is modeled using an axisymmetric, discrete rigid surface. Contact with the rubber is enforced by defining a contact pair between this rigid surface and a surface defined on the (deformable) shell mesh in the contacting region. The metal disks are assumed to be rigid relative to the rubber component of the airspring. The lower metal disk is modeled using boundary conditions, while the upper disk is modeled as part of the rigid surface. The meshes of the rubber membrane and the rigid surface are shown in Figure 3.

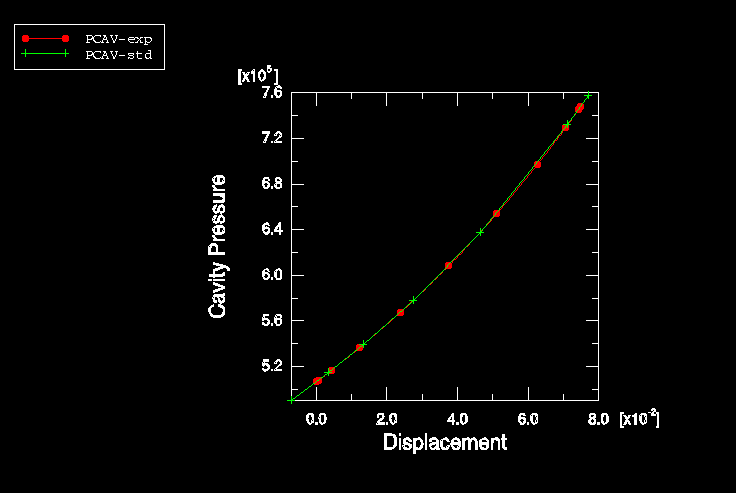
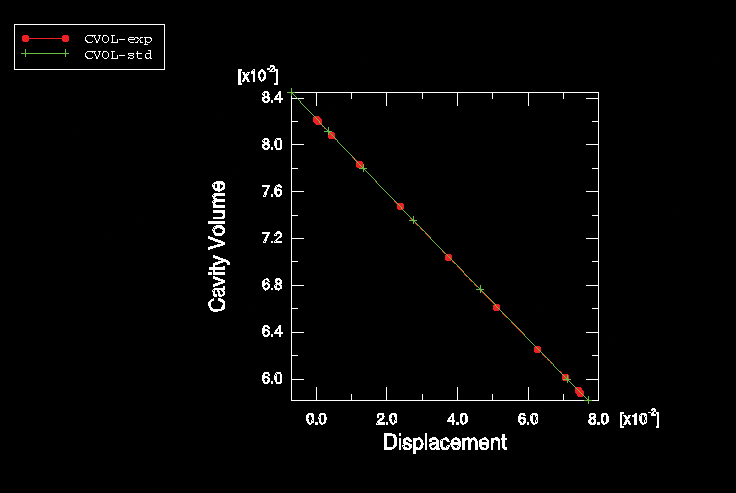
The fluid cavity is modeled using the surface-based fluid cavity capability (see About Surface-Based Fluid Cavities). To define the cavity completely and to ensure proper calculation of its volume, surface elements are defined in the three-dimensional models along the bottom and top rigid disk boundaries of the cavity, even though no displacement elements exist along those surfaces. Since Abaqus does not provide two-dimensional surface elements, the rigid disk boundaries are modeled with structural elements instead of surface elements in the axisymmetric models. The cavity reference node 50000 has a single degree of freedom representing the pressure inside the cavity. Because of symmetry only half of the cavity boundary has been modeled. The cavity reference node has been placed on the model's symmetry plane, y = 0, to assure proper calculation of the cavity volume. Figure 4 shows the mesh of the airspring's cavity.

To facilitate comparisons, the two-dimensional axisymmetric model uses the same cross-sectional mesh refinement as the 180° model. The rubber component is modeled with 25 SAX1 shell elements. The circular bead is modeled with an element-based rigid surface constructed of RAX2 rigid elements. Contact with the hose is enforced by defining a contact pair between this rigid surface and a surface defined on the (deformable) shell mesh in the contacting region. Once again, the lower rigid metal disk is modeled by boundary conditions, and the upper rigid metal disk is modeled as part of the rigid body. The mesh of the rubber membrane and the contact main surface is shown in Figure 5, and the mesh of the cavity is shown in Figure 6. For the membrane model the SAX1 elements are replaced with either MAX1 elements or MGAX1 elements.

Symmetry boundary conditions and initial shell curvature

Symmetry is exploited in the three-dimensional airspring model, and the plane y = 0 is a plane of symmetry. Accurate definition of the initial curvature of the surface being modeled is required, especially on the plane of symmetry. If the user does not provide this information by specifying the normal to the surface at the shell nodes, Abaqus estimates the normal direction based on the coordinates of the surrounding nodes on the shell. Normals computed in this fashion will be inaccurate on the symmetry plane: they will have out-of-plane components, which may lead to inaccurate results. To avoid these difficulties, direction cosines are specified for all shell nodes in the model.

Material properties

The walls of an airspring's rubber component are made from plies of symmetrically placed, positively and negatively oriented reinforcement cords. The walls of an actual component are made of several such layers. However, for the purposes of the three-dimensional example problem being considered, the airspring's wall is taken to be a rubber matrix with a single 6-mm-thick symmetric layer of positively and negatively oriented cords. The cords are modeled by uniformly spaced skew rebar in the shell elements. The rebar are assumed to be made of steel. The rubber is modeled as an incompressible Mooney-Rivlin (hyperelastic) material with $C_{10}$ = 3.2 MPa and $C_{01}$ = 0.8 MPa, and the steel is modeled as a linear elastic material with E = 210.0 GPa and $ν$ = 0.3.

Skew rebar orientations in shell elements are defined by giving the angle between the local 1-axis and the rebar. The default local 1-direction is the projection of the global x-axis onto the shell surface (see Conventions). It is for this reason, and to make the rebar definition uniform for all elements, that the axis of revolution of the airspring model has been chosen to be the global x-axis. Two rebar layers, PLSBAR and MNSBAR, have been defined with orientation angles of 18° and −18°, respectively. The cross-sectional area of the rebar is 1 mm², and they are spaced every 3.5 mm in the shell surface.

The above rebar specification is simplified and somewhat unrealistic. The reinforced plies used in the manufacture of the airspring are located in an initially cylindrical tube with uniform rebar angles. However, the transformation of these layers from a cylindrical geometry to a toroidal one gives the airspring a variable rebar angle and rebar spacing that is dependent on the radius from the axis of revolution of the torus and on the initial rebar angle (see Fursdon, 1990). Hence, a more realistic simulation would require different rebar definitions in each ring of elements in the airspring model.

In the axisymmetric shell model the airspring walls are modeled by a three-layer composite shell section. The two outer layers are each 2.5 mm thick and made up of the same Mooney-Rivlin material that is used in the 180° model. The middle “rebar” layer is 1 mm thick and is made up of an orthotropic elastic material that captures the mechanical behavior of the positively and negatively oriented rebar definition used in the three-dimensional airspring model.

The plane stress orthotropic engineering constants are obtained by looking at the response of a typical element in the three-dimensional model (element 14) subjected to uniaxial extensions along the local 1- and 2-directions. Using a shell thickness of 1 mm, the in-plane states of stress and strain resulting from these two tests are


Test	$ε_{1}$	$ε_{2}$	$σ_{1}$ (MPa)	$σ_{2}$ (MPa)
1-direction	1.00 × 10⁻²	−8.75 × 10⁻²	2.48 × 10¹	−2.41 × 10⁻⁵
2-direction	−1.05 × 10⁻³	1.00 × 10⁻²	−5.96 × 10⁻⁶	2.86 × 10⁻¹

For a plane-stress orthotropic material the in-plane stress and strain components are related to each other as follows:

(\begin{matrix} ε_{1} \\ ε_{2} \end{matrix}) = (\begin{matrix} 1 / E_{1} & - ν_{12} / E_{1} \\ - ν_{21} / E_{2} & 1 / E_{2} \end{matrix}) (\begin{matrix} σ_{1} \\ σ_{2} \end{matrix}),

where $E_{1}$ , $E_{2}$ , $ν_{12}$ , and $ν_{21}$ are engineering constants. Solving for these constants using the above stress-strain relation and the results of the two uniaxial tests yields

\begin{matrix} E_{1} & ​ = 2.48 \times 10^{3} MPa \\ E_{2} & ​ = 2.86 \times 10^{1} MPa \end{matrix}

\begin{matrix} ν_{12} & ​ = 9.1 \\ ν_{21} & ​ = 0.1 \end{matrix}

The remaining required engineering constants— $G_{12}$ , $G_{13}$ , and $G_{23}$ —play no role in the rebar layer definition. Consequently, they have been arbitrarily set to be equal to the shear modulus of the rubber, which is given by $2 (C_{10} + C_{01})$ .

For the axisymmetric membrane model the bulk material is chosen to have the same material properties (Mooney-Rivlin hyperelastic) as those used in the 180° model and the axisymmetric shell model. The rebar parameters and material properties are chosen such that they capture the initial material properties of the sandwiched steel layer in the axisymmetric shell model. The principal material directions do not rotate in the axisymmetric shell model (they are the default element basis directions—the meridional and the hoop directions, respectively). However, they do rotate with finite strain in the axisymmetric membrane model as a result of the use of rebar. Initial stresses are applied to the rebar in the axisymmetric membrane model.

In all analyses the air inside the airspring cavity has been modeled as an ideal gas with molecular weight of 0.044 kg and molar heat capacity of 30 J/kg °K.

Loading

In the Abaqus/Standard model the airspring is first pressurized to 506.6 × 10³ kPa (5 atms) while holding the upper disk fixed. This pressure is applied by prescribing boundary degree of freedom 8 at the cavity reference node. In this case the air volume is adjusted automatically to fill the cavity.

In the next step the prescribed boundary condition on the pressure degree of freedom is removed, thus sealing the cavity with the current air volume. In addition, during this step the boundary condition on the vertical displacement degree of freedom of the rigid body reference node is removed, and in its place a downward load of 150 kN is applied.

The next step is a static linear perturbation procedure. In the axisymmetric model two load cases are considered: one tests the axial stiffness of the airspring with the cavity pressure allowed to vary (closed cavity conditions) and the other tests its axial stiffness with the cavity pressure fixed. The linear perturbation step in the three-dimensional analysis contains three load cases, all under variable cavity pressure (closed cavity) conditions: the first tests the axial stiffness of the airspring, the second tests its lateral stiffness, and the third tests its rotational stiffness for rocking motion in the symmetry plane.

The axisymmetric analysis concludes with a general step in which the airspring is compressed by increasing the downward load to 240.0 kN. The three-dimensional analysis concludes with a general step in which the airspring is subjected to a lateral displacement of 20 mm.

The loading for the Abaqus/Explicit model is similar to that for the Abaqus/Standard model, except for the linear perturbation steps. The airspring is first pressurized to 506.6 × 10³ kPa (5 atms) while holding the upper disk fixed. In the next step the boundary condition on the pressure degree of freedom is removed, thereby sealing the cavity with the current air volume. In addition, for both the axisymmetric and three-dimensional models, the boundary condition on the vertical displacement degree of freedom of the rigid body reference node is modified, so that a downward displacement is applied. This is in contrast to the Abaqus/Standard axisymmetric analysis, where a force was applied. Since the airspring is pressurized, a sudden change in applied force would cause a sudden change in acceleration and induce a low frequency transient response. As a result, the simulation time required for the transient effects to diminish would be very long. Hence, we apply a displacement instead of a force. In the axisymmetric analysis the downward displacement is chosen to be 75 mm, so that the increase in pressure is close to the increase seen in Step 4 of the Abaqus/Standard axisymmetric analysis. The lateral displacement in the three-dimensional Abaqus/Explicit analysis is set to 20 mm so that the results from this step can be compared with those from Step 4 of the Abaqus/Standard three-dimensional analysis.

Results and discussion

Figure 7 and Figure 8 show displaced shape plots of the axisymmetric shell model at the end of the pressurization step. It is of interest to compare the results from this model with those from the 180° model to validate the material model that was used for the rebar reinforcements in the axisymmetric model. A close look at the nodal displacements reveals that the deformation is practically identical for the axisymmetric and three-dimensional models. The results are also virtually identical between corresponding Abaqus/Standard and Abaqus/Explicit models. Moreover, the axial reaction force at the rigid body reference node is 156 kN for the axisymmetric model and 155 kN for the 180° model (after multiplication by a factor of 2). The cavity volume predicted by the axisymmetric model is 8.22 × 10⁻² m³ versus 8.34 × 10⁻² m³ for the 180° model (again, after multiplication by a factor of 2).

Linearized stiffnesses for the airspring are obtained from the Abaqus/Standard linear perturbation load cases. The stiffness is computed by dividing the relevant reaction force at the rigid body reference node by the appropriate displacement. For the axisymmetric model the airspring's axial stiffness under variable cavity pressure conditions is 826 kN/m; its axial stiffness under fixed cavity pressure conditions is 134 kN/m. The difference in axial stiffness between these two cases (a factor of 6) is the result of differences in cavity pressure experienced during axial compression. Under variable cavity pressure conditions, a fixed mass of fluid (air) is contained in a cavity whose volume is decreasing; thus, the cavity pressure increases. Under fixed cavity pressure conditions, the pressure is prescribed as a constant value for the load case. For the 180° model the predicted stiffnesses under variable cavity pressure are as follows: the axial stiffness is 821 kN/m, the lateral stiffness is 3.31 MN/m, and the rotational stiffness is 273 kN/m.

Figure 9 shows a series of displaced shape plots associated with the compression of the axisymmetric Abaqus/Standard airspring model during Step 4. For comparison, Figure 10 shows a series of displaced shape plots associated with the compression of the axisymmetric Abaqus/Explicit model during Step 2. Figure 11 shows the corresponding load-deflection curves. Although the displacement of the rigid body in the Abaqus/Explicit analysis was applied over a short time period (which caused significant inertial effects in the model), there is still good agreement between the slope of the load-displacement curves from the two analyses. The response of the airspring is only slightly nonlinear; consequently, there is good agreement between the axial stiffness obtained with the linear perturbation load case and that obtained from the slope of the load-displacement curve. Figure 12 shows a plot of cavity pressure versus the downward displacement of the rigid body in Step 4 of the Abaqus/Standard analysis and Step 2 of the Abaqus/Explicit analysis. The gauge pressure in the cavity increases by approximately 50% during this step. This pressure increase substantially affects the deformation of the airspring structure and cannot be specified as an externally applied load during the step since it is an unknown quantity. Figure 13 shows a plot of cavity volume versus the downward displacement of the rigid body in Step 4 of the Abaqus/Standard analysis and Step 2 of the Abaqus/Explicit analysis. The cavity pressure and the cavity volume results from the static Abaqus/Standard analysis and the quasi-static Abaqus/Explicit analysis are virtually identical. The corresponding results from the axisymmetric membrane model (not shown) are also in good agreement with the above results.

Figure 14 shows the displaced shape of the 180° Abaqus/Standard model at the end of Step 4, in which a lateral displacement was applied to the airspring. Figure 15 shows the corresponding displaced shape of the 180° model at the end of Step 2 of the Abaqus/Explicit analysis. Figure 16 shows a plot of the load-displacement curves obtained from these steps. Although there is a certain amount of noise that results from the contact conditions and the coarseness of the mesh, the load-deflection curve shows good agreement between the analyses performed quasi-statically in Abaqus/Explicit and statically in Abaqus/Standard. The Abaqus/Explicit analysis was run in double precision to eliminate some of the noise in the load-displacement curve.

Input files

hydrofluidairspring_s4r.inp: Three-dimensional Abaqus/Standard model using shell elements.
hydrofluidairspring_s4r_surf.inp: Three-dimensional Abaqus/Standard model using shell elements with surface-to-surface contact.
hydrofluidairspring_sax1.inp: Axisymmetric Abaqus/Standard model using shell elements.
hydrofluidairspring_sax1_surf.inp: Axisymmetric Abaqus/Standard model using shell elements with surface-to-surface contact.
airspring_exp_s4r_surfcav.inp: Three-dimensional Abaqus/Explicit model using shell elements.
airspring_exp_sax1_surfcav.inp: Axisymmetric Abaqus/Explicit model using shell elements.
hydrofluidairspring_m3d4.inp: Three-dimensional Abaqus/Standard model using membrane elements.
hydrofluidairspring_m3d4_surf.inp: Three-dimensional Abaqus/Standard model using membrane elements with surface-to-surface contact.
hydrofluidairspring_max1.inp: Axisymmetric Abaqus/Standard analysis using rebar reinforced membrane elements.
hydrofluidairspring_mgax1.inp: Axisymmetric Abaqus/Standard analysis using rebar reinforced membrane elements with twist.
airspring_s4r_gcont_surfcav.inp: Three-dimensional Abaqus/Explicit analysis using shell elements and general contact.

References

Dils, M., “Air Springs vs. Air Cylinders,” Machine Design, May 7, 1992.
Fursdon, P. M. T., “Modelling a Cord Reinforced Component with Abaqus,” 6th UK Abaqus User Group Conference Proceedings, 1990.

Figures