Subspace-based steady-state dynamic tire analysis

A description of the tire being modeled is given in Symmetric results transfer for a static tire analysis. In this example we exploit the symmetry in the tire model and utilize the results transfer capability in Abaqus to compute the footprint solution for the full three-dimensional model in a manner identical to that discussed in Symmetric results transfer for a static tire analysis.

Once the footprint solution has been computed, several steady-state dynamic steps are performed. Both direct-solution steady-state dynamic analysis and subspace-based steady-state dynamic analysis are used. Besides being used to validate the subspace projection results, the direct steady-state procedure allows us to demonstrate the computational advantage afforded by the subspace projection capability in Abaqus.

The model used in this analysis is essentially identical to that used in the first simulation discussed in Symmetric results transfer for a static tire analysis, with CGAX4H and CGAX3H elements used in the axisymmetric model and rebar in the continuum elements for the belts and carcass. In addition, instead of using a nonuniform discretization about the circumference, the uniform discretization shown in Figure 1 is used.

The incompressible hyperelastic material used to model the rubber includes a viscoelastic component described by a 1-term Prony series of the dimensionless shear relaxation modulus:

with relaxation coefficient ${\overline{g}}_1^P=0.3$ and relaxation time ${\tau }_1=0.1$. Since the material is incompressible, the volumetric behavior is time independent. This time domain description of the material must be written in the frequency domain to perform a steady-state dynamic analysis. By applying a Fourier transform, the expressions for the time-dependent shear modulus can be written in the frequency domain as follows:

where $G_s\left(\omega \right)$ is the storage modulus, $G_{\mathrm{\ell }}\left(\omega \right)$ is the loss modulus, and $\omega$ is the angular frequency. Abaqus will perform the conversion from time domain to frequency domain automatically if the Prony series parameters are defined. See Time Domain Viscoelasticity for a more detailed discussion on frequency domain viscoelasticity.

The loading sequence for computing the footprint solution is identical to that discussed in Symmetric results transfer for a static tire analysis, with the axisymmetric model contained in tiredynamic_axi_half.inp, the partial three-dimensional model in tiredynamic_symmetric.inp, and the full three-dimensional model in tiredynamic_freqresp.inp. Since geometric nonlinearity is accounted for in the static steps used in computing the footprint solution, the steady-state dynamic analyses, which are linear perturbation procedures, are performed about the nonlinear deformed shape of the footprint solution.

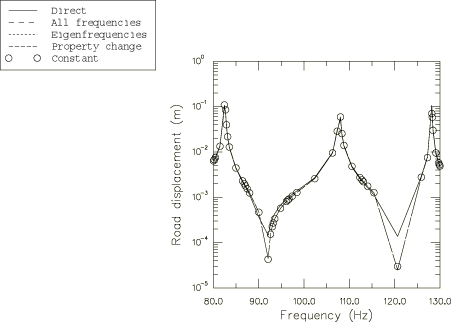
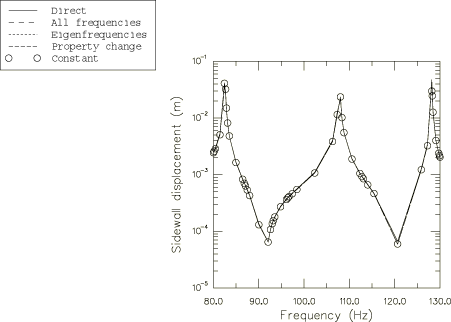
The first frequency response analyses of the tire are performed using the subspace-based steady-state dynamic analysis. The excitation is due to a harmonic vertical load of 200 N, which is applied to the analytical rigid surface through its reference node. The frequency is swept from 80 Hz to 130 Hz. The rim of the tire is held fixed throughout the analysis. Prior to the subspace analysis being performed, the eigenmodes that are used for the subspace projection are computed in an eigenfrequency extraction step. In the frequency step the first 20 eigenpairs are extracted, for which the computed eigenvalues range from 50 to 185 Hz.

The accuracy of the subspace analysis can be improved by including some of the stiffness associated with frequency-dependent material properties—i.e., viscoelasticity—in the eigenmode extraction step. In general, if the material response does not vary significantly over the frequency range of interest, the frequency extraction can be set to evaluate properties at the frequency in the center of the frequency span. Otherwise, more accurate results will be obtained by running several separate frequency analyses over smaller frequency ranges. In this example a single frequency sweep is performed to evaluate properties at 105 Hz.

The main advantage that the subspace projection method offers over mode-based techniques (Mode-Based Steady-State Dynamic Analysis) is that it allows frequency-dependent material properties, such as viscoelasticity, to be included directly in the analysis. However, there is a cost involved in assembling the projected equations, and this cost must be taken into account when deciding between a subspace solution and a direct solution. Abaqus offers four methods to control how often the projected subspace equations are recomputed. These methods are computing the projected equations for every frequency in the analysis, recomputing projected equations only at the eigenfrequencies, recomputing projected equations when the stiffness and/or damping properties have changed by a user-specified percentage, and computing the projected equations only once at the center of the frequency range specified in the steady-state dynamic step. Computing the projected equations for every frequency is, in general, the most accurate option; however, the computational overhead associated with recomputing the projected equations at every frequency can significantly reduce the cost benefit of the subspace method versus a direct solution. Computing the projected equations only once at the center of the frequency range is the most inexpensive choice, but it should be chosen only when the material properties do not depend strongly on frequency. In general, the accuracy and cost associated with the four subspace projection methods are strongly problem dependent. In this example problem the results and computational expense for all four subspace projection methods are discussed.

The results from the various subspace analyses are compared to the results from a direct-solution steady-state dynamic analysis.