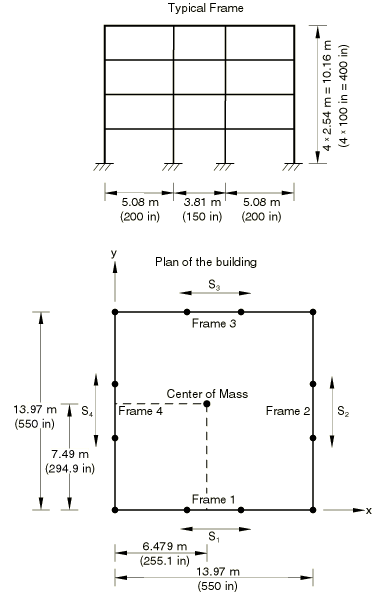
Geometry and model
A four-story steel-frame building based on the frame described in the referenced paper (Wilson and Kiureghian, 1981) is analyzed. By closely matching the geometric dimensions, we can reasonably compare results.
All columns in the building have the same geometric properties. However, as shown in Figure 1, the properties of the beams in Frames 1 and 2 are different, as compared to those in Frames 3 and 4, to move the center of mass of the structure away from its geometric center. Eigenvalue extraction performed on the model shows that many of the 30 modes that cover the frequency range up to 40 Hz are closely spaced. An acceleration spectrum based on the El Centro earthquake record is applied in the x–y plane. The Fortran program given in frameresponsespect_acc.f is used to generate the spectrum. The frequency range is chosen between 0.1 Hz and 40 Hz, and the number of points at which the spectrum is calculated is set at 501. Only one spectrum curve is requested for 2% damping.