Typical Applications
Cohesive elements are useful in modeling adhesives, bonded interfaces, gaskets, and rock fracture. The constitutive response of these elements depends on the specific application and is based on certain assumptions about the deformation and stress states that are appropriate for each application area. The nature of the mechanical constitutive response might broadly be classified to be based on:
-
a continuum description of the material;
-
a traction-separation description of the interface; or
-
a uniaxial stress state appropriate for modeling gaskets and/or laterally unconstrained adhesive patches.
Each of these constitutive response types is discussed briefly below.
Continuum-Based Modeling
The modeling of adhesive joints involves situations where two bodies are connected together by a glue-like material (see Figure 1). A continuum-based modeling of the adhesive is appropriate when the glue has a finite thickness. The macroscopic properties, such as stiffness and strength, of the adhesive material can be measured experimentally and used directly for modeling purposes (see Defining the Constitutive Response of Cohesive Elements Using a Continuum Approach for details). The adhesive material is generally more compliant than the surrounding material. The cohesive elements model the initial loading, the initiation of damage, and the propagation of damage leading to eventual failure in the material.
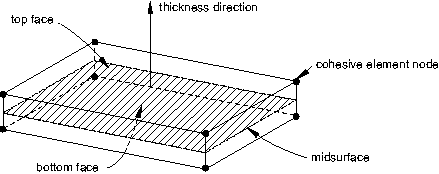
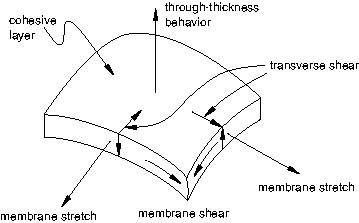
In three-dimensional problems the continuum-based constitutive model assumes one direct (through-thickness) strain, two transverse shear strains, and all (six) stress components to be active at a material point. In two-dimensional problems it assumes one direct (through-thickness) strain, one transverse shear strain, and all (four) stress components to be active at a material point.
Traction-Separation-Based Modeling
The modeling of bonded interfaces in composite materials often involves situations where the intermediate glue material is very thin and for all practical purposes might be considered to be of zero thickness (see Figure 2).
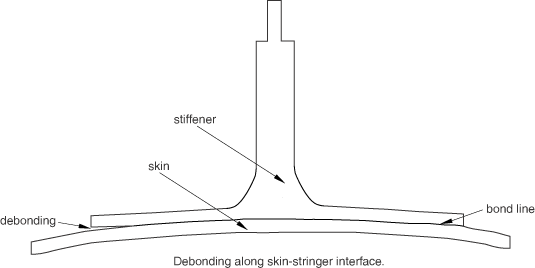
In this case the macroscopic material properties are not relevant directly, and the analyst must resort to concepts derived from fracture mechanics—such as the amount of energy required to create new surfaces (see Defining the Constitutive Response of Cohesive Elements Using a Traction-Separation Description for details). The cohesive elements model the initial loading, the initiation of damage, and the propagation of damage leading to eventual failure at the bonded interface. The behavior of the interface prior to initiation of damage is often described as linear elastic in terms of a penalty stiffness that degrades under tensile and/or shear loading but is unaffected by pure compression.
You may use the cohesive elements in areas of the model where you expect cracks to develop. However, the model need not have any crack to begin with. In fact, the precise locations (among all areas modeled with cohesive elements) where cracks initiate, as well as the evolution characteristics of such cracks, are determined as part of the solution. The cracks are restricted to propagate along the layer of cohesive elements and will not deflect into the surrounding material.
In three-dimensional problems the traction-separation-based model assumes three components of separation—one normal to the interface and two parallel to it; and the corresponding stress components are assumed to be active at a material point. In two-dimensional problems the traction-separation-based model assumes two components of separation—one normal to the interface and the other parallel to it; and the corresponding stress components are assumed to be active at a material point.
Modeling of Gaskets and/or Laterally Unconstrained Adhesive Patches
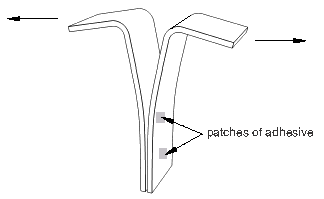
Cohesive elements also provide some limited capabilities for modeling gaskets (see Figure 3).
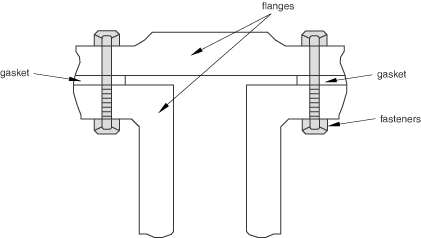
The constitutive response of gaskets modeled with cohesive elements can be defined using only macroscopic properties such as stiffness and strength (see Defining the Constitutive Response of Cohesive Elements Using a Continuum Approach for details). No specialized gasket behavior (typically defined in terms of pressure versus closure) is available. Compared to the class of gasket elements available in Abaqus/Standard (About Gasket Elements), the cohesive elements
-
are fully nonlinear (can be used with finite strains and rotations);
-
can have mass in a dynamic analysis; and
-
are available in both Abaqus/Standard and Abaqus/Explicit.
It is assumed that the gaskets are subjected to a uniaxial stress state. A uniaxial stress state is also appropriate for modeling small adhesive patches that are unconstrained in the lateral direction.
Any material model in Abaqus that is available for use with a one-dimensional element (beams, trusses, or rebars)—including, for example, the hyperelastic and the elastomeric foam material models (useful in this context for modeling gaskets, sealants, or shock absorbers made out of poron)—can be used with this approach.