Problem description
The cantilever is 10 m long. A circular pipe cross-section of outer radius 0.1 m and wall thickness 0.01 m is used for closed-section beam elements so that the beam is moderately slender (100). This type of problem becomes considerably more difficult numerically as the slenderness ratio increases. The standard beam elements in Abaqus should have little difficulty up to slenderness ratios of 1000, but above that the hybrid elements are usually required. However, for this example we have elected to use hybrid elements throughout since they result in better convergence for problems where the beam remains inextensible—in this case, the moment load problem, and to a certain degree, the transverse load problem. Young's modulus is chosen as 100 MPa. The model consists of three elements for the transverse load case and either 10 or 20 elements for the moment load problem, depending on whether linear or quadratic elements are used.
Open-section beam elements of type B31OS, B32OS, B31OSH, and B32OSH can be used with ARBITRARY, GENERAL, and I section types. To test these elements, the cross-section is defined as an I-beam with a height of 200 mm, a width of 100 mm, and web and flange thicknesses of 10 mm. An additional degree of freedom (7) defines the amplitude of the cross-sectional warping. Since the problems considered here are two-dimensional, the torsion and warping considerations are irrelevant.
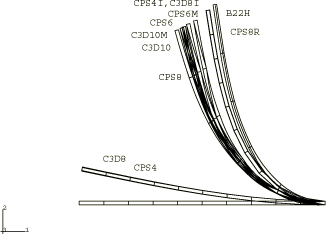
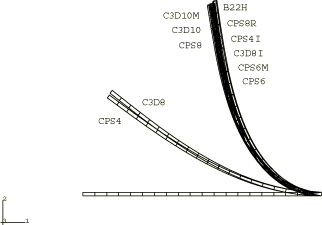
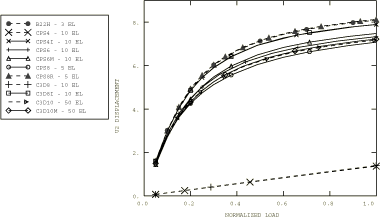
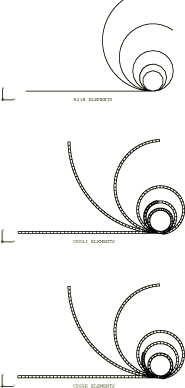
For the continuum elements the solid section thickness and height are chosen to be 100 mm and 147.8 mm, respectively, so that the section moment of inertia is identical to that of the pipe section defined above. The section moment of inertia determines the bending behavior, which is the dominant deformation for both cases since axial deformation is insignificant. We measure the performance of the incompatible mode elements, CPS4I and C3D8I; the second-order elements, CPS8, CPS8R, CPS6, CPS6M, C3D10, C3D10HS, and C3D10M; and the first-order elements, CPS4, CPS4R, C3D8, and C3D8R. The corresponding second-order three-dimensional elements, C3D20 and C3D20R, are not included but can be expected to provide about the same results as the CPS8 and CPS8R elements, respectively. A single layer of elements is used in all the meshes. The reduced-integration, linear elements, CPS4R and C3D8R, when used with enhanced hourglass control give good results that match the results obtained using incompatible mode elements since both are based on an assumed strain formulation. Two mesh types are used for the transverse load case: a coarse mesh of 1 × 10 for the first-order elements and 1 × 5 for the second-order elements and a fine mesh of 1 × 20 for the first-order elements and 1 × 10 for the second-order elements. For the moment load case a 1 × 40 mesh is used with the element types tested (CPS4I, CPS4R, CPS8R, CPS6, CPS6M, and C3D8R). A fine mesh is needed to converge to the correct result; for this loading case a 1 × 20 mesh results in a noticeably stiffer response.
For comparison purposes, reduced-integration linear membrane (M3D4R), shell (S4R), and continuum shell (SC8R) elements are used with enhanced hourglass control for the transverse load and moment load cases with the same meshes as for CPS4R elements. In addition, continuum shell meshes are provided for the transverse load and moment load cases with similar meshes as for C3D8R elements.