Problem description
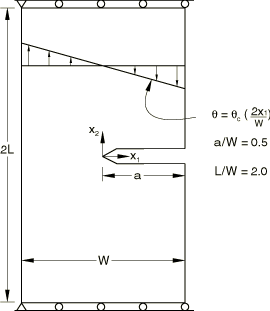
The problem is the case for which Shih et al. (1986) provide results. The example is a single-edged notched specimen, restrained against axial motion at its ends and subjected to a linear temperature variation across its width. The particular geometry studied is cracked halfway through its thickness; the total length of the specimen (2L) is 2.032 m (80 in), and the total width is 508 mm (20 in). The geometry and thermal loading are shown in Figure 1.
The material is isotropic and linear elastic, with a Young's modulus 207 GPa (30 × 106 lb/in2), a Poisson's ratio 0.3, and a thermal expansion coefficient 1.35 × 10−5 per °C (7.5 × 10−6 per °F).
The temperature gradient is given about a mean temperature change of zero. If the mean temperature change were nonzero, the fixed axial end restraints and, in the plane strain case, the thickness direction constraint would induce severe thermal straining.
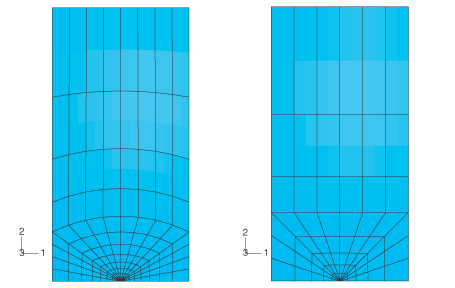
The two focused meshes that are used are shown in Figure 2. Although using elements with curved edges is not recommended in J-integral calculations, the error for this fine a mesh is negligible. The coarser mesh does not contain any curved elements. Due to symmetry, only the top half of the specimen is modeled. In the coarse mesh model there are six rings of elements around the crack tip; thus, J-integral values on at most six contours can be obtained. In the fine mesh model with nine rings of elements around the crack tip, J-integral output can be obtained for nine contours.
The relative path independence of the J-integral values does not prove that the mesh is adequate. In a linear problem approximate path independence of J-integral values can be achieved before the requirements of mesh convergence are met. Mesh convergence is best checked by reanalysis with a finer mesh.
The temperature distribution is obtained by solving a steady-state heat transfer problem, using a mesh of equivalent heat transfer elements, and prescribing the surface temperatures on the two vertical edges of the specimen. Abaqus makes it straightforward to read such temperature solutions into stress analysis models: this technique of thermal-stress analysis is illustrated in Quenching of an infinite plate. The procedure shown in that case could be used to analyze this specimen for the case of a thermal shock, if required.
The heat transfer and thermal-stress analysis can also be done simultaneously with the thermally coupled analysis procedure. This is convenient in the sense that only a single run needs to be made but has the disadvantage that the analysis cost of a thermally coupled analysis can be considerably higher than the cost of sequentially running a heat transfer and thermal-stress analysis, particularly for more complex problems.