Contour integral evaluation: two-dimensional case

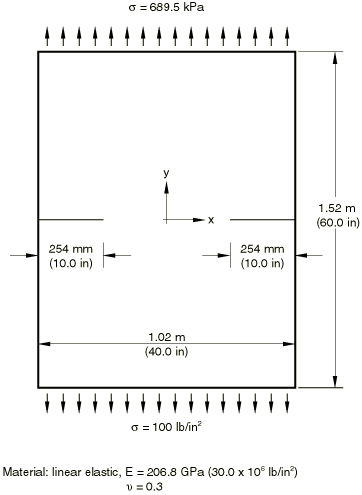
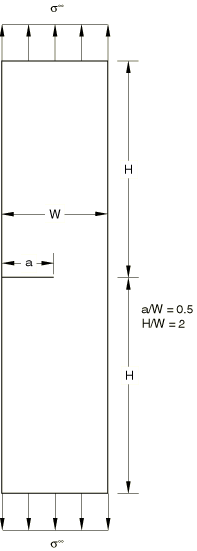
The geometry of the first example is shown in Figure 1. The plane strain structure is a section of a plate with symmetric edge cracks at its centerline, leaving an uncracked ligament of half the plate's width. The specimen is loaded in Mode I by uniform tension applied to its top and bottom surfaces. 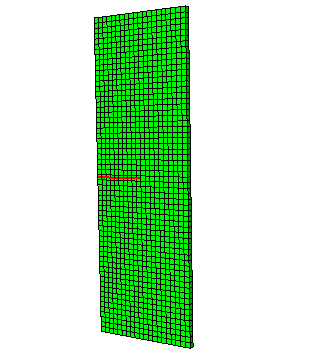When the conventional finite element method is used, symmetry about x = 0 and about y = 0 can be used to model only the top right-hand quadrant of the plate. The mesh used for the quarter model is shown in Figure 2. Second-order elements (8-node quadrilaterals, 20-node bricks) are used. In the case of the full-model seam crack, left and right contour integrals are defined in Abaqus/CAE, as shown in Figure 3. Either the normal to the crack extension or the q vectors can be used to define the crack extension direction.

One advantage of using second-order elements with the conventional finite element method is that they can be used to model the desired singularity at the crack tip. To obtain a $1/\sqrt{r}$ singularity term, the following conditions must be met:

1. The elements around the crack tip must be focused on the crack tip. One edge of each element must be collapsed to zero length (as shown in Figure 2) so that the nodes of this zero length edge are located at the crack tip.

2. The “midside” nodes of the edges radiating out from the crack tip of each of the elements attached to the crack tip must be placed at one-quarter of the distance from the crack tip to the other node of the edge.

The region around the crack tip can be partitioned as shown in Figure 4 and swept meshed with elements having a quad-dominated shape. The node connectivity table is adjusted internally by Abaqus/CAE to create the degenerate quadrilateral elements.

If the coincident nodes at the crack tip are constrained to displace together, the only singularity term in strain is $1/\sqrt{r}$; if the crack-tip nodes are free to displace independently, the crack-tip singularity in strain includes a $1/r$ term in addition to the $1/\sqrt{r}$ term. These methods of creating singularities in standard isoparametric elements are explained in detail by Barsoum (1976).

The material type determines the singularity at the crack tip. A linear elastic material exhibits a $1/\sqrt{r}$ singularity in strain at a sharp crack tip, whereas a perfectly plastic material exhibits a $1/r$ singularity in strain. The singularity in strain for a plastic hardening material lies somewhere between $1/\sqrt{r}$ and $1/r$.

Frequently the need for meshing simplicity with a preprocessor is greater than the need for extreme accuracy of contour integral results. The contour integral results often will be adequate as long as some singularity is included. For example, a $1/r$ singularity is introduced if the element edges are collapsed, the nodes at the crack tip are free to displace independently, and the midside nodes are not moved to the quarter points (they remain at the midside points). This singularity is often quite adequate for elastic-plastic problems.

The model in this example problem uses a linear elastic material and, thus, should be modeled with only a $1/\sqrt{r}$ singularity term.

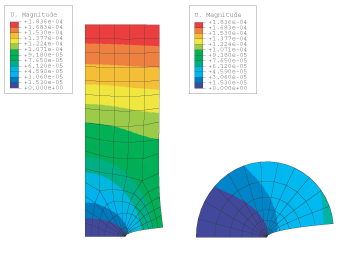
For the quarter model of the double-edged notch specimen, symmetry is used for calculating the contour integral results. Thus, the results for the contour integrals are multiplied by two before being output. The three-dimensional model uses the same mesh with one layer of 20-node bricks, as shown in Figure 5. The loading applied is either a uniform edge load in two dimensions or a uniform surface pressure (of negative magnitude) in three dimensions.

When the extended finite element method is used, the mesh is not required to match the cracked geometry. The presence of a crack is ensured by the special enriched functions in conjunction with additional degrees of freedom. This approach also removes the requirement to explicitly define the crack front or to specify the virtual crack extension direction when evaluating the contour integral. The data required for the contour integral will be determined automatically based on the level set signed distance functions at the nodes in an element. First-order brick elements with both full integration and reduced integration are used for this example. The mesh is shown in Figure 6.

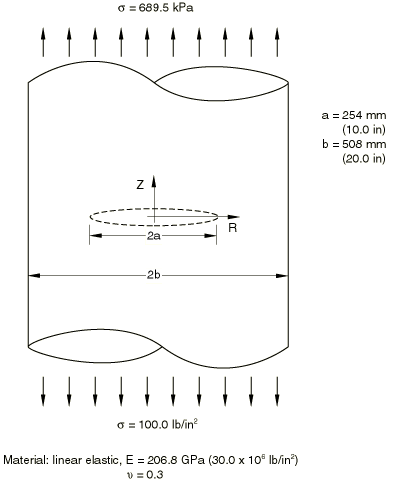
The axisymmetric model corresponds to a penny-shaped crack in a round bar. The model is shown in Figure 7 and is loaded in Mode I by uniform tension applied to the top and bottom surfaces. Symmetry about r = 0 and z = 0 allows you to model only the top right-hand quadrant with a mesh, as shown in Figure 8. Second-order elements (CAX8 and CAX8R) are used.

The third example is a single-edged notch specimen under Mode I tension, as shown in Figure 9. This specimen contains a crack in the symmetry plane in a homogeneous linear elastic material. This example has been studied using both the conventional finite element method and the extended finite element method. Due to symmetry only the top half-plane is modeled for the specimen when used with the conventional finite element method. The complete body is modeled when used with the extended finite element method. Second-order elements CPE8 and CPS8 are used with the conventional finite element method, while first-order brick elements C3D8 and first-order tetrahedral elements C3D4 are used with the extended finite element method.

The last example is also a single-edged notch specimen under Mode I tension, as shown in Figure 9. This specimen contains a crack lying along the interface between two dissimilar elastic materials. The complete body is modeled for the specimen with an interface crack. Second-order elements CPE8 and CPS8 are used for this example.

The J-integral, stress intensity factors, and T-stress should be path independent, and Abaqus provides for its evaluation on as many contours as you request. The first contour is normally at the crack tip, and subsequent contours are generated automatically as contours passing through the nearest neighboring elements, moving out from the crack tip. The mesh used in this case has several rings of elements surrounding the crack tip and as many contours as the number of rings that can be requested. The contour integral should be path independent, so the variation of values between contours can be taken as an indicator of the quality of the mesh for determining the fracture parameters. Path independence of the contour integral values is sufficient to indicate mesh convergence for stress, strain, or displacements.

The submodeling technique is capable of providing a more accurate analysis of the stresses around the crack tip. The global model has a coarse mesh, while the submodel has a refined mesh. For the double-edged notch specimen and the single-edged notch specimen, the submodel region is a semicircular region of radius 127 mm (5 inches). Thus, the submodel boundary is the same as the partition around the crack tip in the global model. The submodel uses a focused mesh with six rows of elements around the crack tip. For the axisymmetric penny crack specimen, the submodel region is a semicircular region of radius 114.3 mm (4.5 inches) and coincides with the outer partition around the crack tip in the global model. The global mesh in all three problems gives satisfactory J-integral results; hence, we assume that the displacements at the submodel boundary are sufficiently accurate to drive the deformation in the submodel. No attempt has been made to study the effect of making the submodel region larger or smaller. The meshed global model with the boundary of the submodel (in dashed lines) is shown on the left, and on the right an enlarged view of the submodel is shown in Figure 10 and Figure 11 for the double-edged notch specimen and the axisymmetric penny crack specimen, respectively.

Contours of the vertical displacement field in the submodel and the global model are shown for a double-edged notch specimen in Figure 12. The continuity of the contour lines verifies that the proper displacement values are prescribed on the submodel boundary. Contour integral values are calculated using five contours. The results of the J-integral are listed in Table 9. The J-integral results obtained with the global mesh are quite accurate; hence, only minor improvements in J-integral values are expected. The same trend also prevails for the calculated stress intensity factor $K_I$ and the T-stress. The agreement with Bowie's approximate solution is indeed slightly better, and a somewhat better path independence can be observed as well. A submodel analysis is also carried out for the axisymmetric model. The calculated J-integral values for the submodel analysis of the axisymmetric penny crack are listed in Table 10.