Analysis of an anisotropic layered plate

This example illustrates the use of a user-defined coordinate system in the analysis of multilayered, laminated, composite shells. The problem considered in this example is the linear analysis of a flat plate made from two layers oriented at $\pm$ 45°, subjected to a uniform pressure loading. The example verifies simple laminated composite plate analysis. The Abaqus results are compared with the analytical solution given in Spilker et al. (1976). The cross-section is not balanced, so the response includes membrane-bending coupling. Composite failure measures are defined for the plane stress orthotropic material.

This page discusses:

Problem description
Failure measures
Results and discussion
Input files
References
Tables
Figures

Problem description

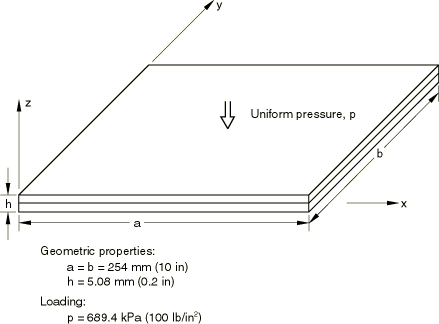
The structure is a two-layer, composite, orthotropic, square plate that is simply supported on its edges. The layers are oriented at $\pm$ 45° with respect to the plate edges. Figure 1 shows the loading and the plate dimensions. Each layer has the following material properties:


$E_{11}$	276 GPa (40 × 10⁶ lb/in²)
$E_{22}$	6.9 GPa (10⁶ lb/in²)
$G_{12} = G_{13} = G_{23}$	3.4 GPa (0.5 × 10⁶ lb/in²)
$ν_{12}$	0.25

These properties define linear elastic behavior for a lamina under plane stress conditions (Linear Elastic Behavior). More general orthotropic properties (for solid continuum elements) can be specified using the elastic stiffness matrix.

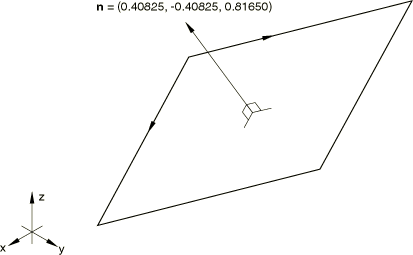
In this example the plate is considered to be at an arbitrary angle to the global axis system to illustrate the use of a local coordinate system. The plate is shown in Figure 2.

The boundary conditions require that displacements that are transverse and normal to the shell edges are fixed, but motions that are parallel to the edges are permitted. A convenient set of local displacement degrees of freedom is defined so that the boundary conditions and the output of nodal variables can be interpreted more easily (Transformed Coordinate Systems).

A local coordinate system is used to define the direction of the layers. The rotation of the material axes of the layers with respect to the standard directions used by Abaqus for stress and strain components in shells is defined in four of the models used and, again for illustration purposes, by means of user subroutine ORIENT in four other models. The section is not balanced since it has only two layers in different orientations, which results in membrane-bending coupling. The motion does not exhibit symmetry for the same reason, and the entire shell must be modeled.

An alternative means of defining the layer orientation is to use a local coordinate to define the orientation of the section and then to define the in-plane angle of rotation relative to the section orientation directly with the layer data in the shell section or general shell section definition. In this case the section force and section strain are calculated in the section orientation directions (rather than the default shell directions).

Three types of models are used. One is an 8 × 8 mesh of S9R5 elements, which are shell elements that allow transverse shear along lines in the element. However, the analytical solution of Spilker et al. uses thin shell theory, which neglects transverse shear effects. We have, therefore, introduced an artificially high transverse shear stiffness in this model.

The second type of model is a 16 × 16 mesh of triangular shells; models for both S3R and SC6R elements are provided. These elements are general-purpose shell elements that allow transverse shear deformation. An artificially high transverse shear stiffness is introduced. No mesh convergence studies have been performed, but finer meshes should improve accuracy since these elements use a constant bending strain approximation.

The third type of model is made up of STRI65 shell elements, which are also based on the discrete Kirchhoff theory. An 8 × 8 mesh is used.

Failure measures

To demonstrate the use of composite failure measures (Plane Stress Orthotropic Failure Measures), limit stresses are defined. The stress-based failure criteria are defined as follows:


$X_{t}$ (Psi)	$X_{c}$ (Psi)	$Y_{t}$ (Psi)	$Y_{c}$ (Psi)	S (Psi)	$\overset{*}{f}$
60.0 × 10⁴	−24.0 × 10⁴	1.0 × 10⁴	−3.0 × 10⁴	2.0 × 10⁴	0.0

Printed failure indices are requested for maximum stress theory (MSTRS) and Tsai-Hill theory (TSAIH). All failure measures are written to the results file (CFAILURE).

Results and discussion

Table 1 summarizes the results by comparing displacement and moment values to the analytical solution. It is clear by the results presented in the table that all models give good results, with the second-order models providing higher accuracy than the first-order S3R model, as would be expected.

Figure 3 shows the failure surface for Tsai-Hill theory (i.e., those stress values $(σ_{11}, σ_{22})$ that, for a given $σ_{12}$ , yield a failure index $R = $ 1.0), along with the stress state at each section point in the center of the plate. Only section point 6 has a stress state outside the failure surface ( $R > $ 1.0).

Input files

anisoplate_s3r_orient.inp: S3R element model with the orientation for the material defined with ORIENTATION.
anisoplate_s3r_usr_orient.inp: S3R element model with the orientation for the material defined in user subroutine ORIENT.
anisoplate_s3r_usr_orient.f: User subroutine ORIENT used in anisoplate_s3r_usr_orient.inp.
anisoplate_sc6r_orient.inp: SC6R element model with the orientation for the material defined with ORIENTATION.
anisoplate_sc6r_usr_orient.inp: SC6R element model with the orientation for the material defined in user subroutine ORIENT.
anisoplate_sc6r_orient_gensect.inp: SC6R model with the orientation for the shell section defined with ORIENTATION and the orientation for the material defined by an angle on the data lines for SHELL GENERAL SECTION.
anisoplate_sc6r_usr_orient.f: User subroutine ORIENT used in anisoplate_sc6r_usr_orient.inp.
anisoplate_s9r5_orient.inp: S9R5 model with the orientation for the material defined with ORIENTATION.
anisoplate_s9r5_usr_orient.inp: S9R5 model with the orientation for the material defined in user subroutine ORIENT.
anisoplate_s9r5_usr_orient.f: User subroutine ORIENT used in anisoplate_s9r5_usr_orient.inp.
anisoplate_s9r5_orient_sect.inp: S9R5 model with the orientation for the shell section defined with ORIENTATION and the orientation for the material defined by an angle on the data lines for SHELL SECTION.
anisoplate_s9r5_orient_gensect.inp: S9R5 model with the orientation for the shell section defined with ORIENTATION and the orientation for the material defined by an angle on the data lines for SHELL GENERAL SECTION.
anisoplate_stri65_orient.inp: STRI65 element model with the orientation for the material defined with ORIENTATION.
anisoplate_stri65_usr_orient.inp: STRI65 element model with the orientation for the material defined in user subroutine ORIENT.
anisoplate_stri65_usr_orient.f: User subroutine ORIENT used in anisoplate_stri65_usr_orient.inp.

References

Spilker, R. L., S. Verbiese, O. Orringer, S. E. French, E. A. Witmer, and A. Harris, “Use of the Hybrid-Stress Finite-Element Model for the Static and Dynamic Analysis of Multilayer Composite Plates and Shells,” Report for the Army Materials and Mechanics Research Center, Watertown, MA, 1976.

Tables

Table 1. Results for pressure loading of anisotropic plate.
Element	In-plane disp. at	Normal disp. at	Moment, $M_{x}$ or $M_{y}$
type	$x = 0, y = b / 2$	center of plate	at center of plate
	(mm)	(mm)	(N-mm)
Analytical	0.3762	23.25	42.05
S3R	0.3724	22.86	40.54
SC6R	0.3724	22.84	40.54
STRI65	0.3760	23.24	42.28
S9R5	0.3752	23.25	42.23

Figures