Stress linearization example | ||
| ||
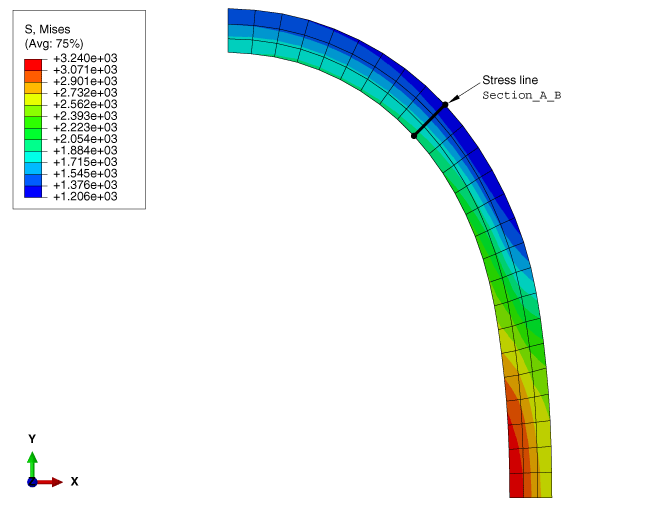
The stress line Section_A_B is defined through the vessel wall. Figure 2 and Figure 3 show the basic settings and computations, respectively, that you use to linearize the S22 stress component for the undeformed model shape.
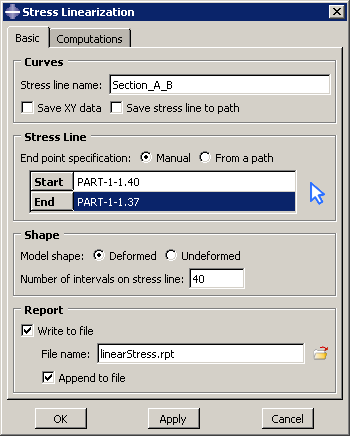
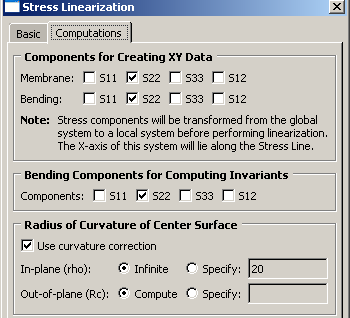
When you click or in the Stress Linearization dialog box, Abaqus/CAE creates an X–Y plot of the S22 stress component (oriented normal to the stress line) and of the resulting linearized stresses, as shown in Figure 4.
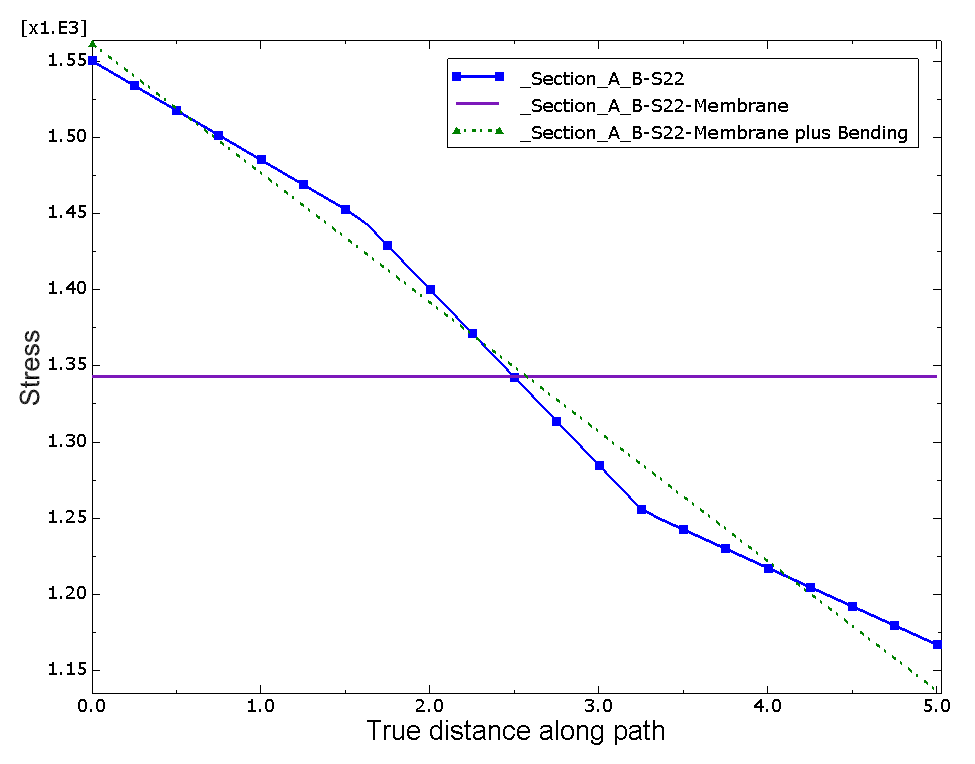
The following output is also written to a file called linearStress.rpt:
********************************************************************************
Statically Equivalent Linear Stress Distribution across a Section,
written on Thu Sep 09 11:20:19 2010
Source
-------
ODB: Job-1.odb
Step: Step-1
Frame: Increment 1: Step Time = 1.000
Linearized Stresses for stress line 'Section_A_B'
Start point, Point 1 - (18.429651260376, 26.8930339813232, 0)
End point, Point 2 - (22.0184745788574, 30.3756923675537, 0)
Number of intervals - 40
------------------------------- COMPONENT RESULTS ------------------------------
S11 S22 S33 S12
0 -462.376 1550.19 1450.75 74.7673
0.125021 -453.722 1542.06 1445.35 74.6265
0.250043 -445.068 1533.93 1439.95 74.4865
0.375064 -436.413 1525.8 1434.55 74.3473
0.500086 -427.759 1517.67 1429.15 74.2089
0.625107 -419.114 1509.55 1423.76 74.0714
0.750128 -410.46 1501.42 1418.36 73.9345
0.87515 -401.806 1493.3 1412.96 73.7983
1.00017 -393.152 1485.17 1407.56 73.663
1.12519 -384.497 1477.04 1402.16 73.5284
1.25021 -375.842 1468.92 1396.76 73.3946
1.37524 -367.187 1460.79 1391.37 73.2615
1.50026 -358.531 1452.67 1385.97 73.1293
1.62528 -348.574 1443.22 1379.7 72.8307
1.7503 -333.79 1428.85 1370.22 71.77
1.87532 -319.007 1414.48 1360.74 70.7052
2.00034 -304.227 1400.1 1351.26 69.6367
2.12536 -289.448 1385.72 1341.78 68.5648
2.25039 -274.656 1371.33 1332.29 67.4908
2.37541 -259.847 1356.91 1322.81 66.4061
2.50043 -245.037 1342.49 1313.32 65.3195
2.62545 -230.228 1328.07 1303.83 64.2284
2.75047 -215.421 1313.64 1294.34 63.1328
2.87549 -200.613 1299.2 1284.84 62.0327
3.00051 -185.807 1284.76 1275.34 60.9282
3.12554 -171.002 1270.32 1265.84 59.8191
3.25056 -156.197 1255.88 1256.34 58.7056
3.37558 -149.216 1248.82 1251.71 57.583
3.5006 -143.031 1242.52 1247.58 56.4609
3.62562 -136.844 1236.21 1243.45 55.34
3.75064 -130.658 1229.91 1239.32 54.2204
3.87566 -124.471 1223.61 1235.19 53.1021
4.00069 -118.283 1217.31 1231.06 51.985
4.12571 -112.095 1211.02 1226.93 50.8691
4.25073 -105.907 1204.72 1222.8 49.7545
4.37575 -99.7185 1198.42 1218.67 48.6412
4.50077 -93.5296 1192.13 1214.55 47.529
4.62579 -87.3403 1185.83 1210.42 46.4182
4.75081 -81.1506 1179.54 1206.3 45.3086
4.87584 -74.9605 1173.25 1202.17 44.2002
5.00086 -68.77 1166.96 1198.05 43.0931
Membrane
(Average) Stress -253.255 1342.83 1317.88 62.6971
Bending
Stress, Point 1 -209.122 218.613 140.324 0
Membrane plus
Bending, Point 1 -462.376 1561.45 1458.2 62.6971
Bending
Stress, Point 2 184.485 -206.054 -140.324 0
Membrane plus
Bending, Point 2 -68.77 1136.78 1177.55 62.6971
Peak Stress,
Point 1 0 -11.2522 -7.44933 12.0701
Peak Stress,
Point 2 0 30.1809 20.4932 -19.604
------------------------------- INVARIANT RESULTS -------------------------------
Bending components in equation for computing
membrane plus bending stress invariants are: S22
Max. Mid. Min. Tresca Mises
Prin. Prin. Prin. Stress Stress
Membrane
(Average) Stress 1345.29 1317.88 -255.714 1601.01 1587.48
Membrane plus
Bending, Point 1 1563.61 1317.88 -255.418 1819.03 1709.46
Membrane plus
Bending, Point 2 1317.88 1139.6 -256.077 1573.95 1492.82
Peak Stress,
Point 1 132.875 -10.5186 -209.855 342.73 298.128
Peak Stress,
Point 2 186.936 27.7292 -119.831 306.767 265.732
The S22 corresponds to the S22 stress shown in Figure 4. The actual stress values plotted in the curve Section_A_B_S22 do not appear in the report. The linearized membrane and membrane-plus-bending stress curves are generated from the values shown for S22. The reported invariants are calculated from the selected linearized components.