Pure bending of a cylinder: CAXA elements

This problem contains basic test cases for one or more Abaqus elements and features.

This page discusses:

Elements tested
Problem description
Results and discussion
Input files
Figures

ProductsAbaqus/Standard

Elements tested

CAXA4n

CAXA4Rn

CAXA8n

CAXA8Rn

(n=1, 2, 3, 4)

Problem description

A hollow cylinder of circular cross-section, inner radius $R_{i}$ , outer radius $R_{o}$ , and length $2 L$ is subjected to a bending moment, M, applied to its end planes. For a linear elastic material with Young's modulus E and Poisson's ratio $ν$ , the solutions for stress and displacement are as follows:

\begin{matrix} σ_{z z} & ​ = \frac{M}{I} r \cos θ \\ σ_{r r} & = σ_{θ θ} = σ_{r z} = σ_{r θ} = σ_{z θ} = 0 \\ u_{r} & ​ = \frac{- M}{2 E I} [z^{2} + ν (r^{2} - R_{i}^{2})] \cos θ \\ u_{θ} & ​ = \frac{M}{2 E I} [z^{2} - ν (r^{2} - R_{i}^{2})] \sin θ \\ u_{z} & ​ = \frac{M}{E I} r z \cos θ, \end{matrix}

where $I = π (R_{o}^{4} - R_{i}^{4}) / 4$ is the moment of inertia of the cylinder and r, $θ$ , and z are the cylindrical coordinates.

Only one-half of the structure is considered, with a symmetry plane at $z = $ 0. The form of the displacement solution, which is a quadratic function in both r and z, suggests that a single second-order element should model the structure accurately. The full- and reduced-integration second-order elements do use a single element mesh, but an 8 × 12 mesh is used for the fully integrated first-order elements and a 16 × 24 mesh is used for the reduced-integration first-order elements.

Material:

Linear elastic, Young's modulus = 30 × 10⁶, Poisson's ratio = 0.33.

Boundary conditions:

$u_{z} = $ 0 on the $z = $ 0 plane; at $r = R_{i}$ on the $z = $ 0 plane, $u_{r}$ at $θ = $ 0° is set equal to $u_{r}$ at $θ = $ 180° with an equation constraint to remove the rigid body motion in the global x-direction.

Loading:

The bending load is simulated by applying a surface traction of the form $σ_{z z} = \frac{M}{I} r \cos θ$ on the $z = L$ plane of the cylinder. This is done by applying the appropriate nonuniform pressure load with a distributed load and defining the variation of the pressure in both the r- and $θ$ -directions with user subroutine DLOAD. In the user subroutine the $θ$ value at each integration point, which is stored in COORDS(3), is expressed in degrees.

Results and discussion

The analytical solution and the Abaqus results for the CAXA8n, CAXA8Rn, CAXA4n, and CAXA4Rn (n=1, 2, 3, or 4) elements are tabulated below for a structure with $\frac{M}{I} = 1$ and dimensions $L = $ 6, $R_{i} = $ 2, and $R_{o} = $ 6. The output locations are at points $A = (R_{i}, 0, 0)$ , $B = (R_{i}, L, 0)$ , $C = (R_{o}, 0, 0)$ , and $D = (R_{o}, L, 0)$ on the $θ = $ 0° plane, as shown in the figure on the previous page, and at points $E, F, G$ , and H, which are at the corresponding locations on the $θ = $ 180° plane. The CAXA8n elements match the exact solution precisely.


Variable	Exact	CAXA8n	CAXA8Rn	CAXA4n	CAXA4Rn
$σ_{z z}$ at A	2	2	2.040	2.102	2.124
$u_{r}$ at A	0	0	0	0	0
$u_{z}$ at A	0	0	0	0	0
$σ_{z z}$ at B	2	2	2	2.098	2.091
$u_{r}$ at B	−6 × 10⁻⁷	−6 × 10⁻⁷	−5.927 × 10⁻⁷	−6.000 × 10⁻⁷	−6.015 × 10⁻⁷
$u_{z}$ at B	4 × 10⁻⁷	4 × 10⁻⁷	4.164 × 10⁻⁷	3.996 × 10⁻⁷	3.984 × 10⁻⁷
$σ_{z z}$ at C	6	6	5.979	5.895	5.877
$u_{r}$ at C	−1.76 × 10⁻⁷	−1.76 × 10⁻⁷	−1.881 × 10⁻⁷	−1.757 × 10⁻⁷	−1.762 × 10⁻⁷
$u_{z}$ at C	0	0	0	0	0
$σ_{z z}$ at D	6	6	6	5.898	5.908
$u_{r}$ at D	−7.76 × 10⁻⁷	−7.76 × 10⁻⁷	−7.954 × 10⁻⁷	−7.757 × 10⁻⁷	−7.779 × 10⁻⁷
$u_{z}$ at D	1.2 × 10⁻⁶	1.2 × 10⁻⁶	1.211 × 10⁻⁶	1.200 × 10⁻⁶	1.203 × 10⁻⁶
$σ_{z z}$ at E	−2	−2	−2.040	−2.102	−2.124
$u_{r}$ at E	0	0	0	0	0
$u_{z}$ at E	0	0	0	0	0
$σ_{z z}$ at F	−2	−2	−2	−2.098	−2.091
$u_{r}$ at F	6 × 10⁻⁷	6 × 10⁻⁷	5.927 × 10⁻⁷	6.000 × 10⁻⁷	6.015 × 10⁻⁷
$u_{z}$ at F	−4 × 10⁻⁷	−4 × 10⁻⁷	−4.164 × 10⁻⁷	−3.996 × 10⁻⁷	−3.984 × 10⁻⁷
$σ_{z z}$ at G	−6	−6	−5.979	−5.895	−5.877
$u_{r}$ at G	1.76 × 10⁻⁷	1.76 × 10⁻⁷	1.881 × 10⁻⁷	1.757 × 10⁻⁷	1.762 × 10⁻⁷
$u_{z}$ at G	0	0	0	0	0
$σ_{z z}$ at H	−6	−6	−6	−5.898	−5.908
$u_{r}$ at H	7.76 × 10⁻⁷	7.76 × 10⁻⁷	7.954 × 10⁻⁷	7.757 × 10⁻⁷	7.779 × 10⁻⁷
$u_{z}$ at H	−1.2 × 10⁻⁶	−1.2 × 10⁻⁶	−1.211 × 10⁻⁶	−1.200 × 10⁻⁶	−1.203 × 10⁻⁶

Note:

The results are independent of n, the number of Fourier modes.

Figure 1 through Figure 4 show plots of the undeformed mesh, the deformed mesh, the contours of $u_{r}$ , and the contours of $u_{z}$ , respectively, for the CAXA4R4 model.

Input files

ecnssfsk.inp: CAXA41 elements.
ecnssfsk.f: User subroutine DLOAD used in ecnssfsk.inp.
ecntsfsk.inp: CAXA42 elements.
ecntsfsk.f: User subroutine DLOAD used in ecntsfsk.inp.
ecnusfsk.inp: CAXA43 elements.
ecnusfsk.f: User subroutine DLOAD used in ecnusfsk.inp.
ecnvsfsk.inp: CAXA44 elements.
ecnvsfsk.f: User subroutine DLOAD used in ecnvsfsk.inp.
ecnssrsk.inp: CAXA4R1 elements.
ecnssrsk.f: User subroutine DLOAD used in ecnssrsk.inp.
ecntsrsk.inp: CAXA4R2 elements.
ecntsrsk.f: User subroutine DLOAD used in ecntsrsk.inp.
ecnusrsk.inp: CAXA4R3 elements.
ecnusrsk.f: User subroutine DLOAD used in ecnusrsk.inp.
ecnvsrsk.inp: CAXA4R4 elements.
ecnvsrsk.f: User subroutine DLOAD used in ecnvsrsk.inp.
ecnwsfsk.inp: CAXA81 elements.
ecnwsfsk.f: User subroutine DLOAD used in ecnwsfsk.inp.
ecnxsfsk.inp: CAXA82 elements.
ecnxsfsk.f: User subroutine DLOAD used in ecnxsfsk.inp.
ecnysfsk.inp: CAXA83 elements.
ecnysfsk.f: User subroutine DLOAD used in ecnysfsk.inp.
ecnzsfsk.inp: CAXA84 elements.
ecnzsfsk.f: User subroutine DLOAD used in ecnzsfsk.inp.
ecnwsrsk.inp: CAXA8R1 elements.
ecnwsrsk.f: User subroutine DLOAD used in ecnwsrsk.inp.
ecnxsrsk.inp: CAXA8R2 elements.
ecnxsrsk.f: User subroutine DLOAD used in ecnxsrsk.inp.
ecnysrsk.inp: CAXA8R3 elements.
ecnysrsk.f: User subroutine DLOAD used in ecnysrsk.inp.
ecnzsrsk.inp: CAXA8R4 elements.
ecnzsrsk.f: User subroutine DLOAD used in ecnzsrsk.inp.

Figures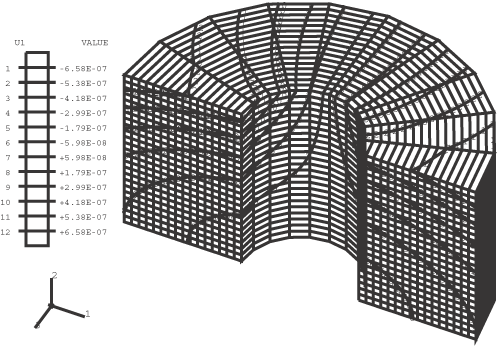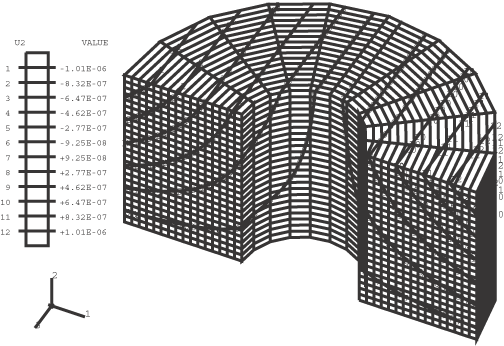