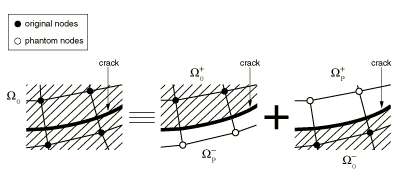
Nodal enrichment functions
For the purpose of fracture analysis, the enrichment functions typically consist of the near-tip asymptotic functions that capture the singularity around the crack tip and a discontinuous function that represents the jump in displacement across the crack surfaces. The approximation for a displacement vector function with the partition of unity enrichment is
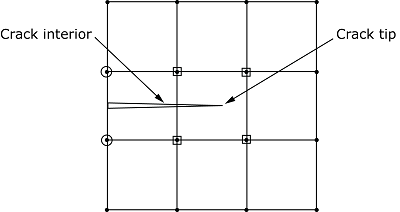

Figure 2 illustrates the discontinuous jump function across the crack surfaces, , which is given by
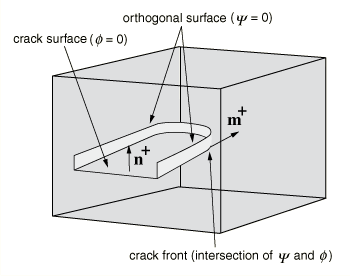
Figure 2 illustrates tangential and normal directions (with respect to the crack) at various points along the interior of the crack, as well as the crack tip. It also illustrates a local polar coordinate system at the crack tip, with respect to which the asymptotic crack tip functions in an isotropic elastic material are given by
As written, these functions span the asymptotic crack-tip function of elastostatics, and takes into account the discontinuity across the crack face. Abaqus/Standard supports singular enrichment functions for isotropic linear elastic materials only. However, the use of asymptotic crack-tip functions is not restricted to crack modeling in an isotropic elastic material. The same approach can be used to represent a crack along a bimaterial interface, impinged on the bimaterial interface, or in an elastic-plastic power law hardening material. In each of these three cases different forms of asymptotic crack-tip functions are employed depending on the crack location and the extent of the inelastic material deformation, as discussed in Sukumar (2004), Sukumar and Prevost (2003), and Elguedj (2006).
Accurately modeling the crack-tip singularity requires constantly keeping track of where the crack propagates, which is cumbersome because the degree of crack singularity depends on the location of the crack in a nonisotropic material. Therefore, we consider the asymptotic singularity functions only when modeling stationary cracks in Abaqus/Standard. When modeling moving cracks, we always assume that the crack must propagate across an entire element at a time to avoid the need to model the near-tip asymptotic singularity. Therefore, only the displacement jump across a cracked element is considered when modeling moving cracks.