Sorption

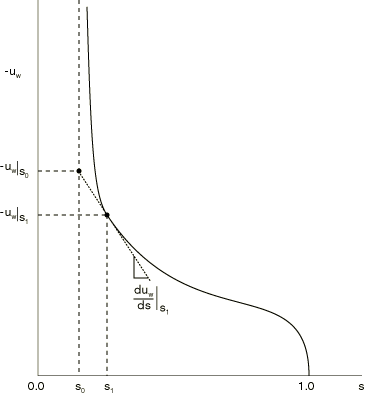
A porous medium becomes partially saturated when the total pore liquid pressure, $u_w$, becomes negative (see Effective stress principle for porous media). Negative values of $u_w$ represent capillary effects in the medium. For $u_w<0$ it is known that the saturation lies within certain limits that depend on the value of the capillary pressure, $-u_w$ (see Continuity statement for the wetting liquid phase in a porous medium). Typical forms of these limits are shown in Figure 1. We write these limits as $s^a\le s\le s^e$, where $s^a\left(u_w\right)$ is the limit at which absorption will occur (so that $\dot{s}>0$), and $s^e\left(u_w\right)$ is the limit at which exsorption will occur (so that $\dot{s}<0$). The transition between absorption and exsorption and vice versa takes place along “scanning” curves (discussed below). These curves are approximated by the single straight line shown in Figure 1.

Figure 1. Typical absorption and exsorption behaviors.

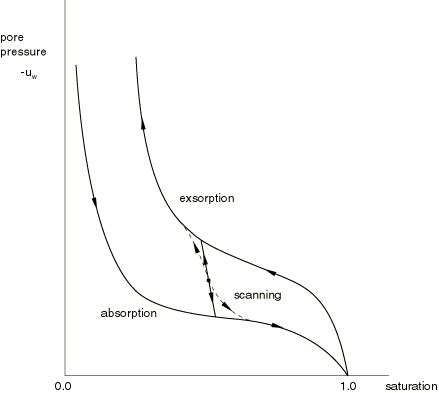
When partial saturation is included in the analysis of flow through a porous medium, the absorption behavior, the exsorption behavior, and the scanning behavior (between absorption and exsorption) should each be defined. Each of these behaviors is discussed below. If sorption is not defined at all, Abaqus/Standard assumes fully saturated flow ($s=1.0$) for all values of $u_w$.

Strongly unsymmetric partially saturated flow coupled equations result from the definition of sorption. Therefore, Abaqus/Standard automatically uses its unsymmetric matrix storage and solution scheme (see Defining an Analysis) if you request partially saturated analysis (i.e., if sorption is defined).

Absorption and exsorption behaviors are defined by specifying the pore liquid pressure, $u_w$ (negative “capillary tension”), as a function of saturation. In most physical cases the wetting liquid cannot be driven to zero saturation; to achieve zero saturation, the data would have to define $u_w\to -\mathrm{\infty }$ as $s\to 0.0$. Absorption and exsorption data can be defined in either a tabular form or an analytical form.

The behavior between absorption and exsorption is defined by a scanning line of user-specified constant slope, ${\left(d{u}_w/ds\right)|}_s$. This slope should be larger than the slope of any segment of the absorption or exsorption behaviors.

If absorption and exsorption behaviors are defined with no scanning line, the slope of the scanning line is taken as 1.05 times the largest value of $d{u}_w/ds$ given in the absorption and exsorption behavior definitions.

SORPTION, TYPE=SCANNING

Property module: material editor: OtherPore FluidSorption: Exsorption: toggle on Include exsorption and Include scanning: Slope ${\left(d{u}_w/ds\right)|}_s$