X–Y plotting | ||
| ||
Context:
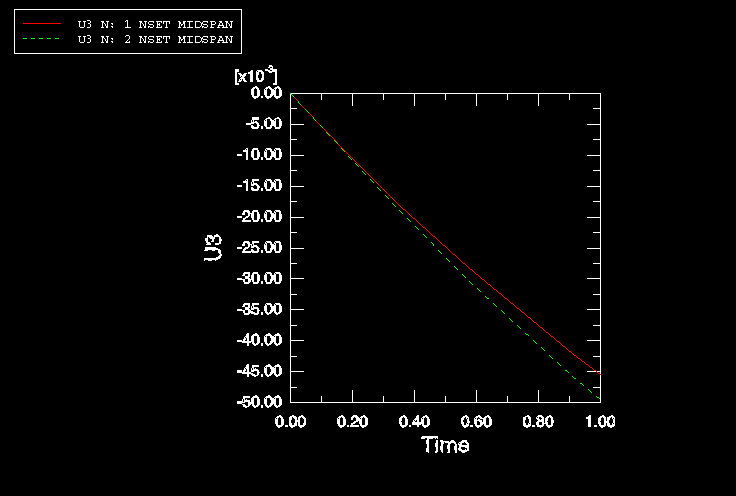
You saved the displacements of the midspan nodes (node set
Midspan) in the history portion of the output
database file NlSkewPlate.odb for each
increment of the simulation. You can use these results to create
X–Y plots. In particular, you will plot the vertical
displacement history of the nodes located at the edges of the plate midspan.