Linear perturbation steps

Linear perturbation analysis steps are available only in Abaqus/Standard.

The starting point for a linear perturbation step is called the base state of the model. If the first step in a simulation is a linear perturbation step, the base state is the state of the model specified using initial conditions. Otherwise, the base state is the state of the simulation at the end of the last general step prior to the linear perturbation step. Although the response of the structure during the perturbation step is by definition linear, the model may have a nonlinear response in previous general steps. For models with a nonlinear response in the prior general steps, Abaqus/Standard uses the current elastic modulus as the linear stiffness for perturbation procedures. This modulus is the initial elastic modulus for elastic-plastic materials and the tangent modulus for hyperelastic materials (see Figure 1); the moduli used for other material models are described in General and Perturbation Procedures.

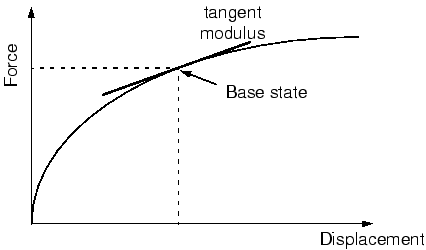
Figure 1. For hyperelastic materials the tangent modulus is used as the stiffness in linear perturbation steps that occur after general, nonlinear steps.

The loads in the perturbation step should be sufficiently small that the model's response would not deviate much from that predicted with the tangent modulus. If the simulation includes contact, by default the contact state between two surfaces does not change during a perturbation step: points that were closed in the base state remain closed, and points that were open remain open. Optionally, contact constraints can be enforced only where the contact pressure in the base state exceeds a specified threshold.

If another general step follows a perturbation step, Abaqus/Standard uses the state of the model at the end of the last general step as its starting point, not the state of the model at the end of the perturbation step. Thus, the response from a linear perturbation step has no permanent effect on the simulation. Therefore, Abaqus/Standard does not include the step time of linear perturbation steps in the total time for the analysis. In fact, what Abaqus/Standard actually does is to define the step time of a perturbation step to be very small (10−36) so that it has no effect when it is added to the total accumulated time. The exception to this rule is the modal dynamics procedure.