Vibrational frequencies analysis

The pipe is made of steel and has an outer diameter of 18 cm and a 2 cm wall thickness (see Figure 1).

Figure 1. Portion of piping system being analyzed.

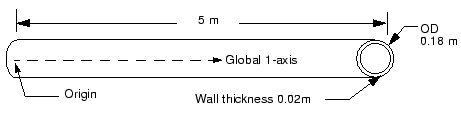
It is clamped firmly at one end and can move only axially at the other end. This 5 m portion of the piping system may be subjected to harmonic loading at frequencies up to 50 Hz. The lowest vibrational mode of the unloaded structure is 40.1 Hz, but this value does not consider how the loading applied to the piping structure may affect its response. To ensure that the section does not resonate, you have been asked to determine the magnitude of the in-service load that is required so that its lowest vibrational mode is higher than 50 Hz. You are told that the section of pipe will be subjected to axial tension when in service. Start by considering a load magnitude of 4 MN.

The lowest vibrational mode of the pipe will be a sine wave deformation in any direction transverse to the pipe axis because of the symmetry of the structure's cross-section. You will use three-dimensional beam elements to model the pipe section.

The analysis requires a natural frequency extraction. Thus, you will use Abaqus/Standard as your analysis product.