Geometric nonlinearity

The third source of nonlinearity is related to changes in the geometry of the structure during the analysis. Geometric nonlinearity occurs whenever the magnitude of the displacements affects the response of the structure. This may be caused by:

  • Large deflections or rotations.

  • “Snap through.”

  • Initial stresses or load stiffening.

For example, consider a cantilever beam loaded vertically at the tip (see Figure 1).

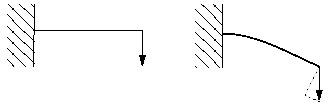
Figure 1. Large deflection of a cantilever beam.

If the tip deflection is small, the analysis can be considered as being approximately linear. However, if the tip deflections are large, the shape of the structure and, hence, its stiffness changes. In addition, if the load does not remain perpendicular to the beam, the action of the load on the structure changes significantly. As the cantilever beam deflects, the load can be resolved into a component perpendicular to the beam and a component acting along the length of the beam. Both of these effects contribute to the nonlinear response of the cantilever beam (i.e., the changing of the beam's stiffness as the load it carries increases).

One would expect large deflections and rotations to have a significant effect on the way that structures carry loads. However, displacements do not necessarily have to be large relative to the dimensions of the structure for geometric nonlinearity to be important. Consider the “snap through” under applied pressure of a large panel with a shallow curve, as shown in Figure 2.

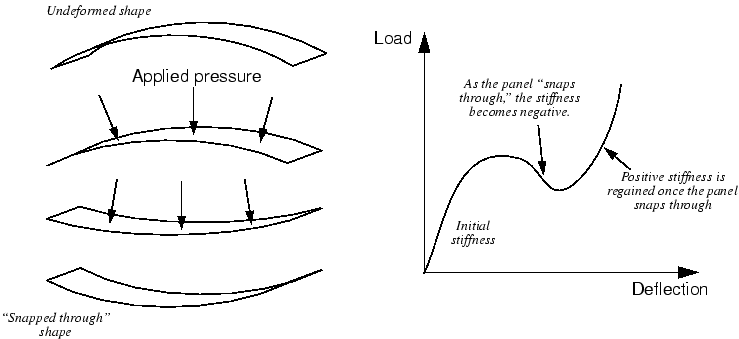
Figure 2. Snap-through of a large shallow panel.

In this example there is a dramatic change in the stiffness of the panel as it deforms. As the panel “snaps through,” the stiffness becomes negative. Thus, although the magnitude of the displacements, relative to the panel's dimensions, is quite small, there is significant geometric nonlinearity in the simulation, which must be taken into consideration.

An important difference between the analysis products should be noted here: by default, Abaqus/Standard assumes small deformations, while Abaqus/Explicit assumes large deformations.