Characteristics of plasticity in ductile metals

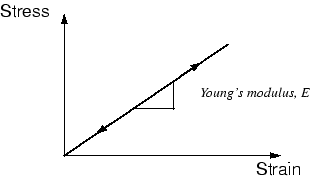
Many metals have approximately linear elastic behavior at low strain magnitudes, and the stiffness of the material, known as the Young's or elastic modulus, is constant.

Figure 1. Stress-strain behavior for a linear elastic material, such as steel, at small strains.

At higher stress (and strain) magnitudes, metals begin to have nonlinear, inelastic behavior (see Figure 2), which is referred to as plasticity.

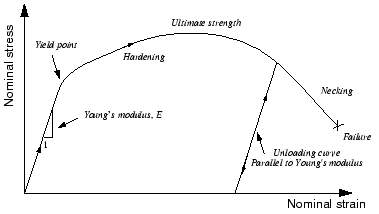
Figure 2. Nominal stress-strain behavior of an elastic-plastic material in a tensile test.

The plastic behavior of a material is described by its yield point and its post-yield hardening. The shift from elastic to plastic behavior occurs at a certain point, known as the elastic limit or yield point, on a material's stress-strain curve (see Figure 2). The stress at the yield point is called the yield stress. In most metals the initial yield stress is 0.05 to 0.1% of the material's elastic modulus.

The deformation of the metal prior to reaching the yield point creates only elastic strains, which are fully recovered if the applied load is removed. However, once the stress in the metal exceeds the yield stress, permanent (inelastic) deformation begins to occur. The strains associated with this permanent deformation are called plastic strains. Both elastic and plastic strains accumulate as the metal deforms in the post-yield region.

The stiffness of a metal typically decreases dramatically once the material yields (see Figure 2). A ductile metal that has yielded will recover its initial elastic stiffness when the applied load is removed (see Figure 2). Often the plastic deformation of the material increases its yield stress for subsequent loadings: this behavior is called work hardening.

Another important feature of metal plasticity is that the inelastic deformation is associated with nearly incompressible material behavior. Modeling this effect places some severe restrictions on the type of elements that can be used in elastic-plastic simulations.

A metal deforming plastically under a tensile load may experience highly localized extension and thinning, called necking, as the material fails (see Figure 2). The engineering stress (force per unit undeformed area) in the metal is known as the nominal stress, with the conjugate nominal strain (length change per unit undeformed length). The nominal stress in the metal as it is necking is much lower than the material's ultimate strength. This material behavior is caused by the geometry of the test specimen, the nature of the test itself, and the stress and strain measures used. For example, testing the same material in compression produces a stress-strain plot that does not have a necking region because the specimen is not going to thin as it deforms under compressive loads. A mathematical model describing the plastic behavior of metals should be able to account for differences in the compressive and tensile behavior independent of the structure's geometry or the nature of the applied loads. This goal can be accomplished if the familiar definitions of nominal stress, F/A0, and nominal strain, Δ⁢l/l0, where the subscript 0 indicates a value from the undeformed state of the material, are replaced by new measures of stress and strain that account for the change in area during the finite deformations.