Definition of damping in Abaqus/Standard
In Abaqus/Standard a number of different types of damping can be defined for a transient modal analysis: direct modal damping, Rayleigh damping, and composite modal damping.
Damping is defined for modal dynamic procedures. The damping is part of the step definition, and different amounts of damping can be defined for each mode.
- Direct modal damping
-
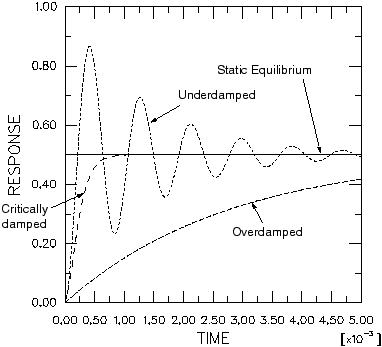
The fraction of critical damping, , associated with each mode can be defined using direct modal damping. Typically, values in the range of 1% to 10% of critical damping are used. Direct modal damping allows you to define precisely the damping of each mode of the system.
- Rayleigh damping
-
In Rayleigh damping the assumption is made that the damping matrix is a linear combination of the mass and stiffness matrices,
where and are user-defined constants. Although the assumption that the damping is proportional to the mass and stiffness matrices has no rigorous physical basis, in practice the damping distribution rarely is known in sufficient detail to warrant any other more complicated model. In general, this model ceases to be reliable for heavily damped systems; that is, above approximately 10% of critical damping. As with the other forms of damping, you can define precisely the Rayleigh damping of each mode of the system.
For a given mode i, the damping ratio, , and the Rayleigh damping values, and , are related through
- Composite damping
-
In composite damping a fraction of critical damping is defined for each material, and a composite damping value is found for the whole structure. This option is useful when many different materials are present in the structure. Composite damping is not discussed further in this guide.