Initial contact overclosure

Abaqus/Explicit will automatically adjust the undeformed coordinates of nodes on contact surfaces to remove any initial overclosures. When using the balanced main-secondary approach, both surfaces are adjusted; when using the pure main-secondary approach, only the secondary surface is adjusted. Displacements associated with adjusting the surface to remove overclosures do not cause any initial strain or stress for contact defined in the first step of the analysis. When conflicting constraints exist, initial overclosures may not be completely resolved by repositioning nodes. In this case severe mesh distortions can result near the beginning of an analysis when the contact pair algorithm is used. The general contact algorithm stores any unresolved initial penetrations as offsets to avoid large initial accelerations.

In subsequent steps any nodal adjustments to remove initial overclosures cause strains that often cause severe mesh distortions because the entire nodal adjustments occur in a single, very brief increment. This is especially true when the kinematic constraint method is used. For example, if a node is overclosed by 1.0 × 10−3 m and the increment time is 1.0 × 10−7 s, the acceleration applied to the node to correct the overclosure is 2.0 × 1011 m/s2. Such a large acceleration applied to a single node typically will cause warnings about deformation speed exceeding the wave speed of the material and warnings about severe mesh distortions a few increments later, once the large acceleration has deformed the associated elements significantly. Even a very slight initial overclosure can induce extremely large accelerations for kinematic contact. In general, it is important that in the second step and beyond any new contact surfaces that you define are not overclosed.

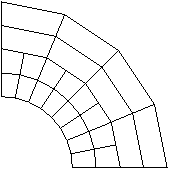
Figure 1 shows a common case of initial overclosure of two contact surfaces. All of the nodes on the contact surfaces lie exactly on the same arc of a circle; but since the mesh of the inner surface is finer than that of the outer surface and since the element edges are linear, some nodes on the finer, inner surface initially penetrate the outer surface.

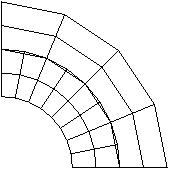
Figure 1. Original overclosure of two contact surfaces.

Assuming that the pure main-secondary approach is used, Figure 2 shows the initial, strain-free displacements applied to the secondary-surface nodes by Abaqus/Explicit. In the absence of external loads this geometry is stress free. If the default, balanced main-secondary approach is used, a different initial set of displacements is obtained, and the resulting mesh is not entirely stress free.

Figure 2. Corrected contact surfaces.