The initial static step, which moves the riser to its offset position and
applies the static loads, is completed in four increments. The first increment
requires more iterations than subsequent increments, which is typical of this
class of problem: the riser is initially unstressed and, therefore, is highly
flexible. After some loading is applied, the axial tension stabilizes the
system, and convergence is more rapid.
At the end of the static step the top of the riser makes an angle of 1.17°
with the vertical. This value agrees well with the value of 1.20° presented in
API
BULLETIN2J (1977). The angle
predicted at the base of the riser is 2.48°, which compares to 2.55° reported
in the API bulletin. The slight discrepancies
are attributed to the relative coarseness of the model.
The dynamic solution is carried out for 18 seconds of response. Typically
one equilibrium iteration is required in each of the time increments.
Half-increment residual values for the first few increments are of order 178 MN
(4.0 × 107 lb), and at the end of the run they are of order 4.4 kN
(1000 lb). This result is typical: initially there is much high frequency
content in the solution, which is reflected in the larger half-increment
residual values. As the analysis proceeds, the fluid drag dissipates this
“noise,” the solution becomes smoother, and the half-increment residual values
drop accordingly.
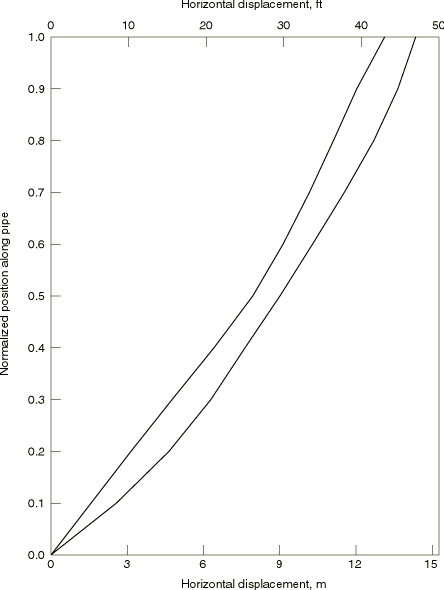
The envelope of pipeline excursions during the second cycle of the dynamic
excitation is plotted in
Figure 2,
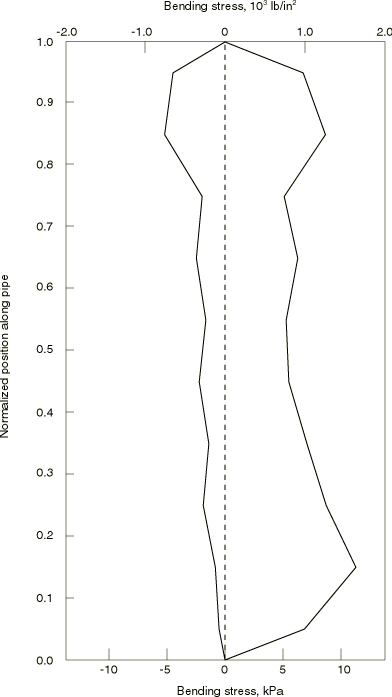
and the envelope of bending stress is shown in
Figure 3.
These results are in basic agreement with those given in the
API bulletin.
As expected, the results obtained by the model with the Airy wave theory
implemented in user subroutine
UWAVE are identical to those due to the built-in Airy wave
option.