Upsetting of a cylindrical billet: quasi-static analysis with mesh-to-mesh solution mapping (Abaqus/Standard) and adaptive meshing (Abaqus/Explicit)

The geometry is the standard test case of Lippmann (1979) and is defined in Upsetting of a cylindrical billet: coupled temperature-displacement and adiabatic analysis. It is a circular billet, 30 mm long, with a radius of 10 mm, compressed between two flat, rigid dies that are defined to be perfectly rough.

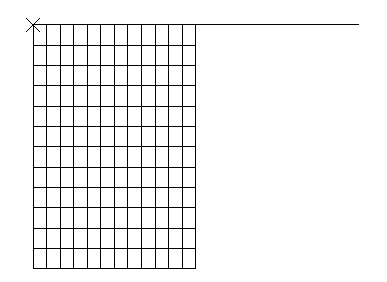
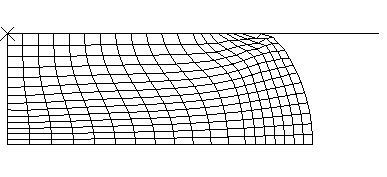
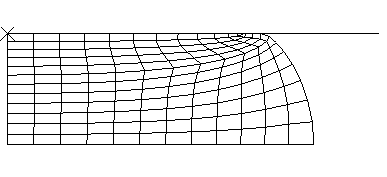
The mesh used to begin the analysis is shown in Figure 1. The finite element model is axisymmetric and includes the top half of the billet only since the middle surface of the billet is a plane of symmetry. In both the Abaqus/Standard and Abaqus/Explicit simulations, element type CAX4R is used: this is a 4-node quadrilateral with a single integration point and “hourglass control” to control spurious mechanisms caused by the fully reduced integration. The element is chosen here because it is relatively inexpensive for problems involving nonlinear constitutive behavior since the material calculations are only done at one point in each element. In addition, in the Abaqus/Standard simulations element types CGAX4R, CGAX4T, CAX4P, and CAX4I are also used to model the billet; in the Abaqus/Explicit simulations element type CAX6M is also used to model the billet.

The contact between the top and lateral exterior surfaces of the billet and the rigid die is modeled with a contact pair in Abaqus/Standard and with general contact in Abaqus/Explicit. The billet surface is specified as a surface definition in the model. The rigid die is modeled in a variety of different ways as described in Table 1. The mechanical interaction between the contact surfaces is assumed to be nonintermittent, rough frictional contact. Therefore, the contact property includes two additional specifications: rough friction to enforce a no-slip constraint between the two surfaces, and a no-separation contact pressure-overclosure relationship to ensure that separation does not occur once contact has been established. All the contact simulations in Abaqus/Standard use the node-to-surface formulation except one case where the surface-to-surface formulation is introduced.

Table 1 summarizes the different analysis cases that are studied. The column headings indicate whether the problem was analyzed using Abaqus/Standard and/or Abaqus/Explicit.

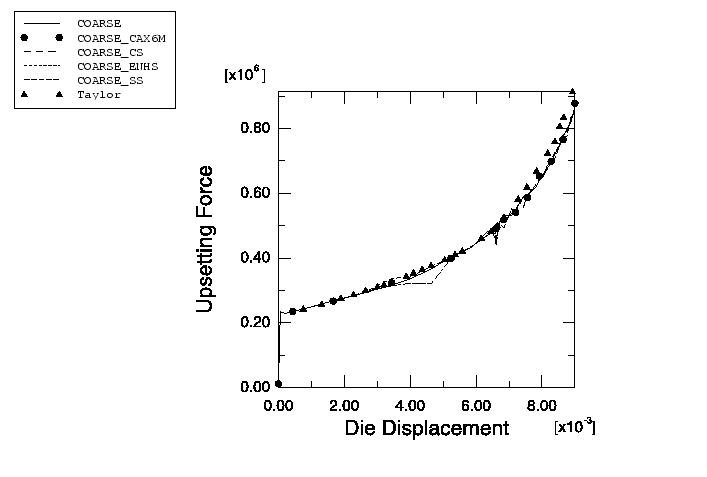
For Case 1 several different analyses are performed to compare the different section control options available in Abaqus/Explicit and to evaluate the effects of mesh refinement for the billet modeled with CAX4R elements. A coarse mesh (analysis COARSE_SS) and a fine mesh (analysis FINE_SS) are analyzed with the pure stiffness form of hourglass control. A coarse mesh (analysis COARSE_CS) is analyzed with the combined hourglass control. A coarse mesh (analysis COARSE_ENHS) and a fine mesh (analysis FINE_ENHS) are analyzed with the hourglass control based on the enhanced strain method. The default section controls, using the integral viscoelastic form of hourglass control, are tested on a coarse mesh (analysis COARSE) and a fine mesh (analysis FINE). Since this is a quasi-static analysis, the viscous hourglass control option should not be used. All other cases use the default section controls.

The Abaqus/Standard analyses for Case 1 compare the two hourglass control options and evaluate the effect of mesh refinement for the billet modeled with CAX4R elements. A coarse mesh (analysis COARSE_S) and a fine mesh (analysis FINE_S) are analyzed with the pure stiffness form of hourglass control. A coarse mesh (analysis COARSE_EH) and a fine mesh (analysis FINE_EH) are analyzed with hourglass control based on the enhanced strain method. A coarse mesh (analysis COARSE_EHG) with CGAX4R elements is also analyzed with hourglass control based on the enhanced strain method for comparison purposes.

No mesh convergence studies have been done, but the agreement with the results given in Lippmann (1979) suggests that the meshes used here are good enough to provide reasonable predictions of the overall force on the dies.

The material model assumed for the billet is that given in Lippmann (1979). Young's modulus is 200 GPa, Poisson's ratio is 0.3, and the density is 7833 kg/m³. A rate-independent von Mises elastic-plastic material model is used, with a yield stress of 700 MPa and a hardening slope of 0.3 GPa.

The kinematic boundary conditions are symmetry on the axis (nodes at $r=$ 0, in node set AXIS, have $u_r=$ 0 prescribed) and symmetry about $z=$ 0 (all nodes at $z=$ 0, in node set MIDDLE, have $u_z=$ 0 prescribed). The node on the top surface of the billet that lies on the symmetry axis is not part of the node set AXIS to avoid overconstraint: the radial motion of this node is already constrained by a no slip frictional constraint (see Common Difficulties Associated with Contact Modeling in Abaqus/Standard and Common Difficulties Associated with Contact Modeling Using Contact Pairs in Abaqus/Explicit).

In Abaqus/Standard the rigid die is displaced by −9 mm in the axial direction using a displacement boundary condition. In Abaqus/Explicit the $u_z$ -displacement of the rigid die is prescribed using a velocity boundary condition whose value is ramped up to a velocity of 20 m/s and then held constant until the die has moved a total of 9 mm. The total simulation time of the Abaqus/Explicit analysis is 0.55 millisec, and the loading rate is slow enough to be considered quasi-static. In both Abaqus/Standard and Abaqus/Explicit the radial and rotational degrees of freedom of the rigid die are constrained.

For all cases the analyses are done in two steps so that the first step can be stopped at a die displacement corresponding to 44% upsetting; the second step carries the analysis to 60% upsetting. In the Abaqus/Standard simulations the solution mapping analysis restarts from the end of the first step with a new mesh and proceeds until 60% upsetting is achieved.

The interpolation technique used in solution mapping is a two-step process. First, values of all solution variables are obtained at the nodes of the old mesh by extrapolating the values from the integration points to the nodes of each element and averaging those values over all elements abutting each node. The second step is to locate each integration point in the new mesh with respect to the old mesh (this assumes all integration points in the new mesh lie within the bounds of the old mesh: warning messages are issued if this is not so, and new model solution variables at the integration point are set to zero). The variables are then interpolated from the nodes of the element in the old mesh to the location in the new mesh. All solution variables are interpolated automatically in this way so that the solution can proceed on the new mesh. Whenever a model is mapped, it can be expected that there will be some discontinuity in the solution because of the change in the mesh. If the discontinuity is significant, it is an indication that the meshes are too coarse or that the mapping should have been done at an earlier stage before too much distortion occurred.

The model is built and meshed using Abaqus/CAE. The solution mapping for the Abaqus/Standard analysis is done by extracting the two-dimensional profile of the deformed billet from the output; the user must enter commands into the command line interface at the bottom of the Abaqus/CAE main window. To extract the deformed geometry from the output database as an orphan mesh part, use the command PartFromOdb, which takes the following arguments:

name

The name of the orphan mesh part to be created.

odb

The output database object returned from the command openOdb.

instance

The name of the part instance in the initial model in capital letters.

shape

Determines whether to import the part in its UNDEFORMED or DEFORMED shape.

The command PartFromOdb returns a Part object that is passed to the command Part2DGeomFrom2DMesh. This command creates a geometric Part object from the orphan mesh imported earlier. It takes the following arguments:

name

The name of the part to be created.

part

The part object returned from the command PartFromOdb.

featureAngle

A float specifying the angle (in degrees) between line segments that triggers a break in the geometry.

Once the profile of the deformed part has been created, the user can switch to the Mesh module, remesh the part, and write out the new node and element definitions to be used in the mapping analysis. The Python script file billet_rezone.py is included to demonstrate the process described above.

Adaptive meshing consists of two fundamental tasks: creating a new mesh, and remapping the solution variables from the old mesh to the new mesh with a process called advection. A new mesh is created at a specified frequency for each adaptive mesh domain. The mesh is found by sweeping iteratively over the adaptive mesh domain and moving nodes to smooth the mesh. The process of mapping solution variables from an old mesh to a new mesh is referred to as an advection sweep. At least one advection sweep is performed in every adaptive mesh increment. The methods used for advecting solution variables to the new mesh are consistent; monotonic; (by default) accurate to the second order; and conserve mass, momentum, and energy. This example problem uses the default settings for adaptive mesh domains.