Fully and sequentially coupled acoustic-structural analysis of a muffler

The fully coupled model includes the effect of the acoustic pressure in the surrounding air loading the muffler body during vibration of the system. When modeling the acoustics of metal structures in air, such as in this case, such acoustic pressure loading is often negligible in comparison with other forces in the structure. The submodeling capability can be used in this situation. The part of the interacting system that is unaffected by the other is treated as the “global” model, while the part whose solution depends strongly on the solution of the other is treated as the “submodel.” In the case of an acoustic analysis, of course, this nomenclature refers to the hierarchy of the solutions, not the geometric sizes of the models.

When sequential coupling is physically appropriate, its use offers a performance advantage over a fully coupled solution. Two problems, each smaller than the fully coupled problem, are less computationally expensive. If the applicability of the sequentially coupled solution method is uncertain, the user should make characteristic test computations in the frequency range of interest. If these computations show little difference between the fully and sequentially coupled solutions, the less expensive sequentially coupled method can be used.

The system considered here consists of a cylindrical muffler and the interacting air. The muffler is a simple tube 180 mm in diameter and 1 m in length, with inlet and outlet pipes 70 mm in diameter and 100 mm in length. The muffler structure is made from stainless steel sheeting, 0.75 mm in thickness. A porous packing material, which dampens the acoustic field, surrounds the inner pipe.

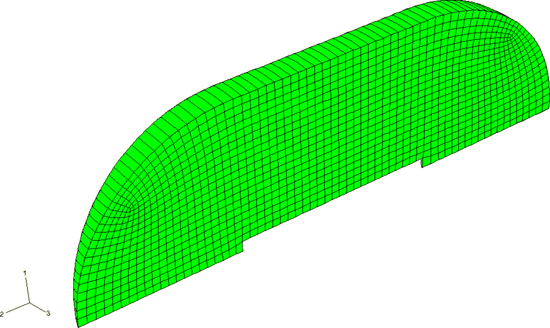
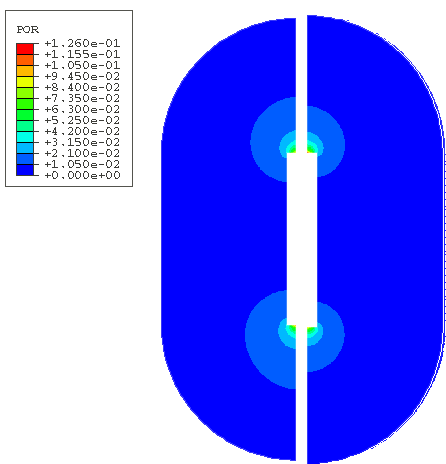
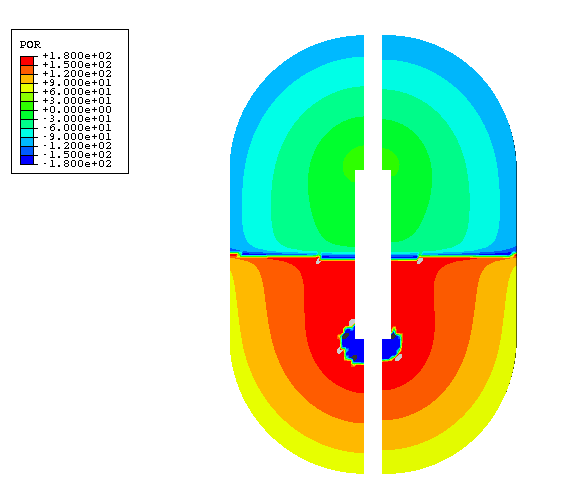
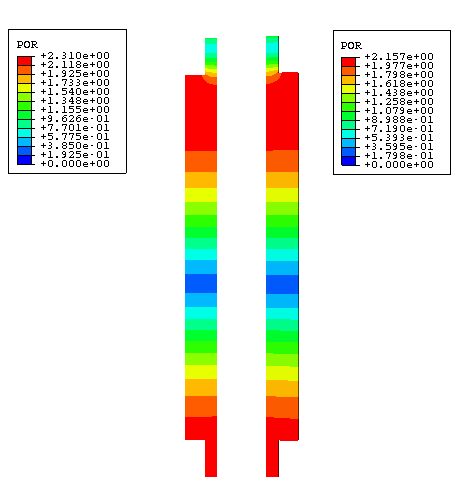
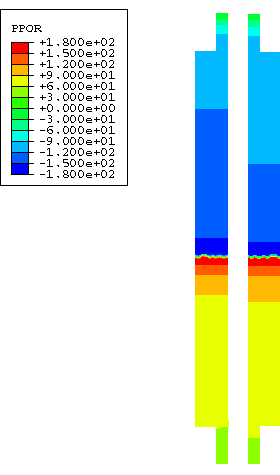
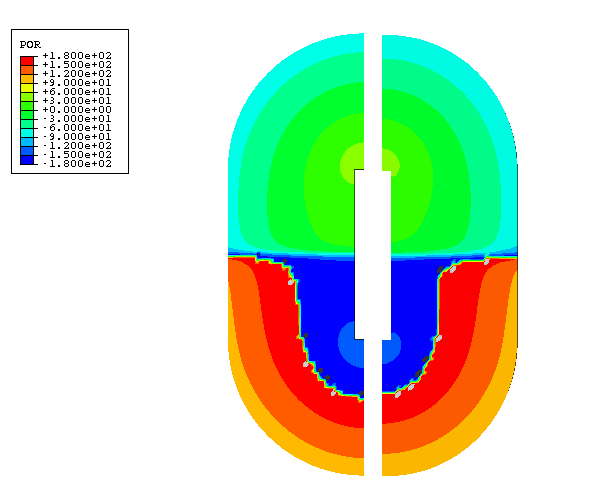
Although this problem is in essence axisymmetric, a narrow three-dimensional wedge (subtending an angle of 10°) of the coupled system is modeled because Abaqus has a limitation on the use of submodeling with axisymmetric shells. Appropriate boundary conditions are applied to the three-dimensional model so that the axisymmetric solution is captured. The meshes of the surrounding air, the exterior muffler shell, and the air inside the muffler are shown in Figure 1, Figure 2, and Figure 3, respectively.

The air inside the muffler is meshed with AC3D10 elements (second-order tetrahedra) in Abaqus/Standard and with AC3D4 elements in Abaqus/Explicit. The innermost column of fluid elements models the undamped air. The adjacent annulus models the air in the region of the packing material. These two regions are highlighted in Figure 3, where the annulus is shown as the darker region. The effect of the packing material is modeled using the volumetric drag coefficient for the acoustic medium. The muffler is meshed with S4R shell elements.

The exterior fluid is shown in Figure 1. Its outer boundary is made up of spherical and cylindrical segments, on which spherical and cylindrical absorbing boundary conditions are imposed. The cylindrical and spherical absorbing boundary conditions can be combined in Abaqus, allowing the external mesh to conform to the geometry of the radiating object more closely. Combinations of different boundary condition types are most effective when the boundaries are continuous in slope as well as displacement. Second-order hexahedral acoustic elements (AC3D20) are used in Abaqus/Standard and reduced-integration acoustic brick elements (AC3D8R) are used in Abaqus/Explicit to fill in the volume of the exterior fluid region.

In Abaqus/Explicit the possibility of using acoustic infinite elements to model the effect of the exterior fluid is explored. The use of acoustic infinite elements removes the need of impedance-type absorbing boundary conditions on the outer boundary. Acoustic infinite elements are used in two different ways. In the first approach the mesh modeling the exterior fluid is replaced by a single row of AC3D8R elements, and acoustic infinite elements ACIN3D4 are defined on the outer boundary of this row. In the second approach ACIN3D4 elements are defined directly on the outer boundary of the muffler and tied to the muffler surface.

In the submodeling procedure performed in Abaqus/Standard the interface between the surrounding air and the muffler is meshed with 8-node acoustic interface elements (ASI8); in the Abaqus/Explicit submodeling analysis the tie constraint is used to define this coupling. The choice of mesh density (element size) is discussed in Acoustic, Shock, and Coupled Acoustic-Structural Analysis. In both cases the inner boundary of the exterior air mesh conforms to the muffler shell and to rigid baffles, which isolate the exterior field from the exhaust and inlet noise. These baffle pipes are the same diameter as the inlet and exhaust pipes but are modeled simply by imposing no boundary condition on the acoustic elements in this region. This is equivalent to imposing the condition that the acceleration on this boundary is zero, which is correct for a rigid baffle.

In Abaqus/Standard we are most interested in performing a frequency sweep about the first resonant frequency of the fully coupled system. For problems involving air and metal structures, the structure usually dominates the behavior of the system. Therefore, an estimate of the first important resonance of the coupled system is found by performing a frequency sweep in the vicinity of the first eigenfrequency of the muffler shell, computed without any interaction with the interior or exterior air. This occurs at f = 172 Hz. Although the resonant frequencies of the fully coupled system do not coincide with the resonant frequencies of the muffler shell alone, they are close, especially at lower frequencies.

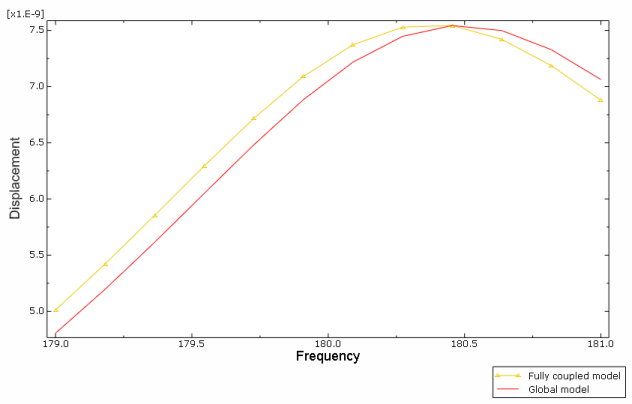
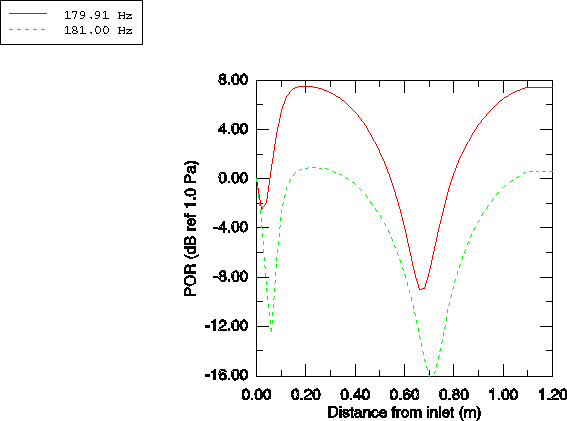
Using the Abaqus/Standard direct-solution steady-state dynamic procedure to search around 172 Hz, we find that the first resonant frequency for the fully coupled system occurs at approximately 180 Hz. A frequency sweep of both the fully coupled and the sequentially coupled models from 179.0 Hz to 181.0 Hz at 0.2 Hz increments is performed. A pressure wave of unit magnitude is applied to the muffler inlet at each frequency, and a plane wave absorbing boundary condition is applied at the muffler outlet.

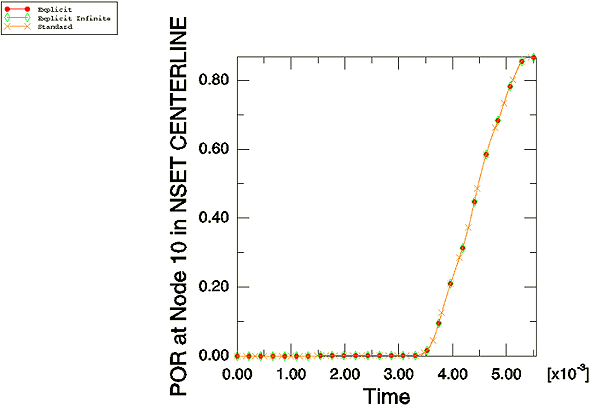
A transient dynamic analysis is performed in Abaqus/Explicit over the period of time that corresponds to the first resonant frequency of 180 Hz found in Abaqus/Standard. The pressure boundary conditions applied at the muffler inlet have a sinusoidal variation over time to simulate the steady-state dynamic procedure performed in Abaqus/Standard. The absorbing boundary conditions are imposed in the same way as in the steady-state dynamic procedure.

The material properties for the air are a bulk modulus $K_f$ of 0.142 MPa and a density ${\rho }_f$ of 1.2 kg/m³, yielding a characteristic sound speed of 344 m/s. The volumetric drag, $\gamma$, specified for the air in the packing material region is 1.2 N s/m. Volumetric drag values are considered “small” if they are small compared to 2$\pi {\rho }_{f}f$, a condition satisfied by $\gamma$ = 1.2 N s/m for the frequency range of interest. The muffler is made of stainless steel with Young's modulus E of 190 GPa, Poisson's ratio $\nu$ of 0.3, and density ${\rho }_s$ of 7920 kg/m³.

Material properties affect the mesh parameters appropriate for wave problems. The characteristic wavelength of air at $f=$ 180 Hz, $\mathrm{\Omega }=2\pi \times 180\approx$ 1131 rad/sec, is ${\lambda }_a=\sqrt{\frac{K_f}{{\rho }_f{f}^2}}\approx$ 1.91 m, which is long compared to the overall system geometry. The internodal spacing of roughly 40 mm used in the surrounding acoustic mesh and 30 mm in the interior acoustic mesh is adequate for this frequency. The acoustic wavelength must also be considered in selecting the overall size of the exterior domain. Accuracy of the solution requires placement of the radiating boundary at least one-quarter wavelength from the acoustic sources; in this problem a standoff distance of approximately 700 mm is selected. The characteristic flexural wavelength ${\lambda }_p$ of the steel plating can be computed using the thickness h and the formula ${\lambda }_p=\frac{2\pi }{\sqrt{\mathrm{\Omega }}}{\left(\frac{E{h}^2}{12{\rho }_s\left(1-{\nu }^2\right)}\right)}^{1/4}\approx$ 203 mm. The discretization requirements of the finite element method in wave problems require at least six nodes per wavelength; here, we use an internodal distance of approximately 30 mm for the shells.

The fully coupled model consists of all three meshes shown in Figure 1, Figure 2, and Figure 3 constrained at their abutting surfaces using a tie constraint.

The sequentially coupled analysis is performed in two jobs. The “global” model job consists of the meshes shown in Figure 2 and Figure 3. The shell displacements, and displacement phases in Abaqus/Standard, are saved from this analysis and drive the second “submodel” analysis through the use of a submodel boundary condition. In Abaqus/Standard the second model consists of the exterior air mesh (Figure 1) used in the fully coupled case, with ASI8 elements placed on the boundary that abuts the shell surface. These elements convert the displacements from the “global” analysis to the appropriate boundary conditions for acoustic elements. In this analysis the ASI8 elements conform to the acoustic submodel mesh but not to the shell mesh of the global model. The nodes of the ASI8 elements are placed in a node set, specified in the model data of the submodel. The global elements used to drive the submodel must be specified to ensure that only the displacements of the ASI8 elements are driven by the shell elements. If this global element set is not specified, Abaqus may attempt to drive the acoustic pressure of the ASI8 elements by the interior acoustic elements, since those elements share the shell nodes in the “global” model. In Abaqus/Explicit the tie constraint is used in both the global and submodel analyses to couple the muffler structure with the surrounding acoustic medium.