Problem description
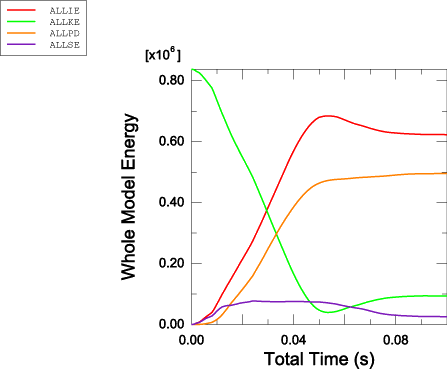
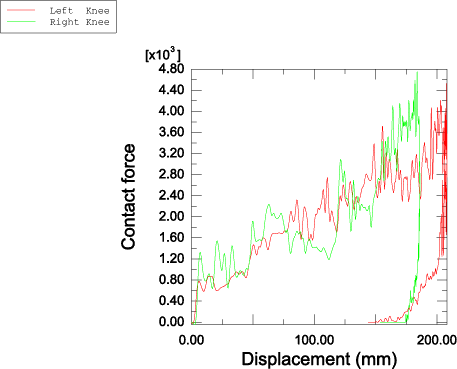
The model represents an automobile knee bolster assembly—the portion of the instrument panel that the occupant's legs impact in the event of a crash. The assembly consists of a hard plastic cover (the knee bolster) supported by a stiff steel substructure. Proper design of this assembly ensures that the occupant's energy is dissipated with a minimum of injury-causing forces. In this simulation the legs approach the knee bolster at 6 m/s, representing unrestrained motion following a 15 mph to dead stop crash event.
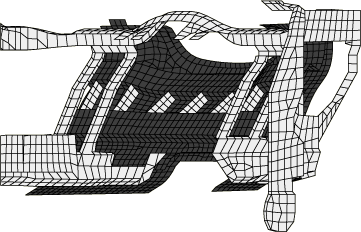
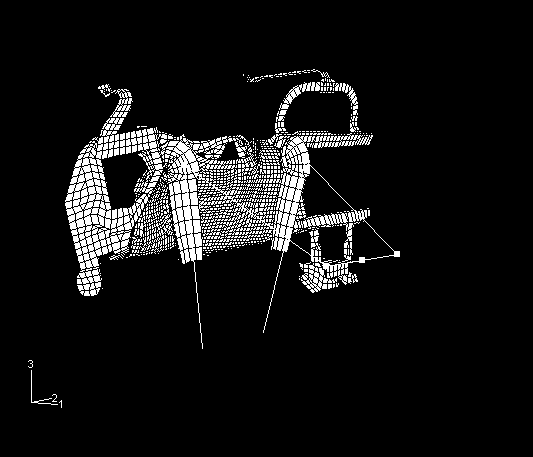
The components of the instrument panel are modeled using S3R and S4R shell elements. The bolster is made up of 2690 shell elements, with the material modeled as a von Mises, elastic strain hardening plastic material with a Young's modulus of 2.346 GPa, a Poisson's ratio of 0.4, a density of 1140 kg/m3, and a yield stress of 11.7 MPa. The steel substructure is made up of 1648 elements, with the material modeled as a strain hardening steel with a Young's modulus of 207 GPa, a Poisson's ratio of 0.3, a density of 7700 kg/m3, and a yield stress of 207 MPa. Figure 1 shows the model geometry from the rear of the knee bolster prior to impact, and Figure 2 shows the knee bolster and knee/leg assembly from a position outboard and behind the driver prior to impact.
The legs are represented as structural members with a surrounding rigid surface. The structural members, representing the bones, are modeled with B31 beam elements and T3D2 truss elements, with the material modeled as elastic with a Young's modulus of 207 GPa, a Poisson's ratio of 0.3, and a density of 7.7 kg/m3. The rigid surfaces, representing the knee and shin, are modeled with R3D4 rigid elements. The body mass is modeled by distributing mass elements at various locations among the nodes of the structural elements.
In the input file knee_bolster_nsm.inp the upper body mass is distributed over the hip bones (B31 beam elements) as a nonstructural mass instead of point masses. The nonstructural mass contribution to an element increases both the element mass and the element rotary inertia, thus resulting in an increased stable time increment. This analysis completes in about 40% fewer increments when the nonstructural mass feature is used since the time increment for the problem is controlled by the beam elements. In the input file knee_bolster_massadjust.inp, the upper body mass is distributed over the hip bones using mass adjustment instead of point masses. The mass distribution and analysis results are similar to those using nonstructural mass. Input files for similar analyses using pipe elements (PIPE31) instead of beam elements are included.
Potential contact among the instrument panel assembly components and between the instrument panel and the legs is modeled using the general contact capability. The general contact inclusions option to automatically define an all-inclusive surface is used and is the simplest way to define contact in the model. In addition, a model that uses the alternative contact pair algorithm is provided; the contact definition is more tedious with the contact pair algorithm.
Initial velocities are defined on the leg components to approximate a 15 mph (6 m/s) crash condition. The hips are constrained to translate in the plane of the seat. The ankles are constrained consistent with fixed planting of the feet on the floor of the car. The dashboard substructure is fixed at locations where it would be welded to the automobile frame; deformations due to this impact are assumed to be confined to the explicitly modeled structure.