Eigenvalue analysis of a piezoelectric transducer

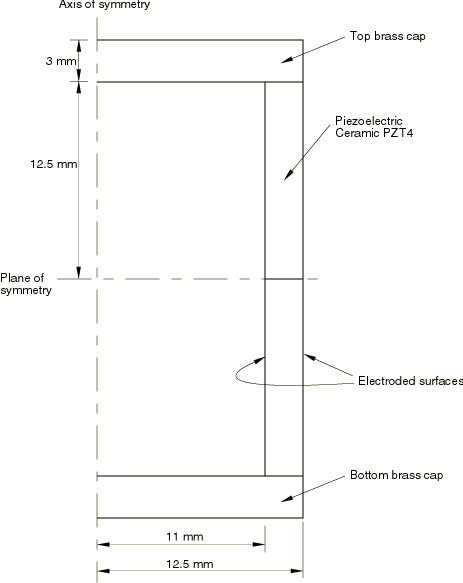
This problem is identical to the one discussed in a report by Mercer et al. (1987). The structure is shown in Figure 1 and consists of a piezoelectric material PZT4 with brass end caps. The piezoelectric material is electroded on both the inner and outer surfaces.

The properties for PZT4 in a cylindrical system are:

Elasticity Matrix:

Piezoelectric Coupling Matrix (Stress Coefficients):

Dielectric Matrix:

The 1-direction is radial, the 2-direction is axial, and the 3-direction is tangential. From these matrices it is seen that the poling direction is radially outwards from the axis of symmetry. (The order of the stresses in Abaqus may differ from those typically used in electrical applications. Abaqus uses the standard mechanical convention, where the stress components are ordered as $\left\{{\sigma }_{11}{\sigma }_{22}{\sigma }_{33}{\tau }_{12}{\tau }_{13}{\tau }_{23}\right\}$. See Piezoelectric Behavior.)

The brass is elastic and isotropic with a Young's modulus of 104 GPa and a Poisson's ratio of 0.37.

The transducer is modeled with a variety of elements. It is modeled as an axisymmetric structure utilizing both the planar, axisymmetric elements and the three-dimensional elements. For the axisymmetric elements, five meshes employing 4-node, 6-node, and 8-node elements are used in the finite element discretization. The first two meshes use 4-node elements with two levels of refinement, the third mesh uses 6-node elements, and the last two meshes use the 8-node elements with two levels of refinement. Lumped mass matrices are used for the lower-order elements. Consistent mass matrices are used in the higher-order elements. The meshes used for the 4-node and 6-node axisymmetric elements are shown in Figure 2. The meshes used for the 8-node axisymmetric elements are shown in Figure 3.

The three-dimensional model uses a slice of the structure and applies axisymmetric boundary conditions; 8-node and 20-node brick elements are used. The discretization used for each model is shown in Figure 3. These models use a local coordinate system to maintain the proper definitions of the material properties. Also, in order to prescribe the axisymmetric boundary conditions, the nodal degrees of freedom are transformed into a cylindrical coordinate system.

All the models are considered to be open-circuited. The potentials on the inside surface are restrained to zero. The frequencies correspond to those for antiresonance.