Application description
This example illustrates topology optimization of an automotive control arm. During a topology optimization, the material properties of the elements in the design area are modified (effectively removing elements from or adding elements to the Abaqus analysis) until the optimal solution is achieved. For more information, see Topology Optimization.
Geometry
The control arm model is a single orphan mesh part that was meshed with quadratic tetrahedral (C3D10) elements. The control arm is symmetric about the X–Y plane, and only one half of the model is studied.
Materials
The control arm is made of an elastic material with a Young's modulus of 210 GPa and a Poisson’s ratio of 0.3.
Boundary conditions and loading
The center of the model is constrained to be symmetric about the Y–Z plane. The upper left and upper right ends of the control arm are outside the design area and are fixed in all three translation degrees of freedom. The lower bearing center is also outside the design area, and its translation is constrained along the z-direction.
The center node of the lower bearing is loaded with a concentrated force of 70000 N in the x-direction and −70000 N in the y-direction.
Optimization features
The topology optimization is configured as described in the following sections.
Optimization task
This example creates a topology optimization task that is governed by the condition-based optimization algorithm.
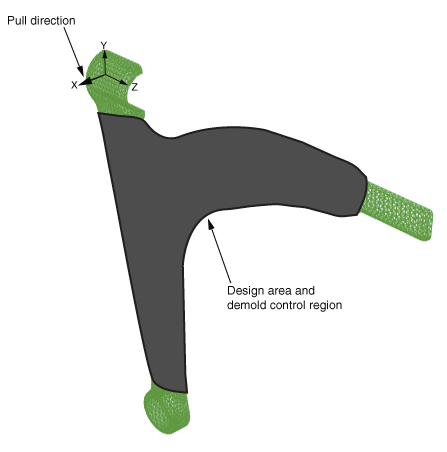
Design area
The design area of the model is the region that will be modified during the optimization, as shown in Figure 1. Some regions are excluded from the design area because they are required for fixtures and for applying loads. The material properties of the elements excluded from the design area remain unchanged.
Design responses
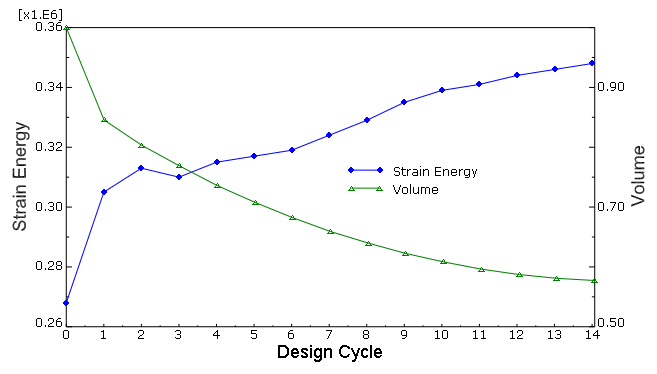
A design response is created that calculates the sum of the strain energy over all the elements in the design area. A second design response calculates the volume of the design area.
Objective function
Objective functions define the objective of the optimization. In this example a single objective function attempts to minimize the sum of the strain energy of the design area. Since compliance is defined as the sum of the strain energy, and stiffness is the reciprocal of compliance, the objective function is equivalent to maximizing the stiffness of the design area.
Constraint
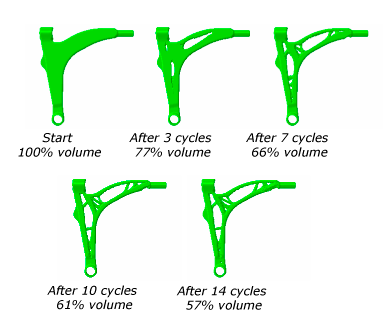
Optimization constraints constrain the optimization process from making changes to the topology of the model. Constraints must allow the optimization to arrive at a solution that is both feasible and acceptable. In this example a single constraint is created that specifies that the optimized model should contain 57% of the initial volume of the original control arm.
Geometry restrictions
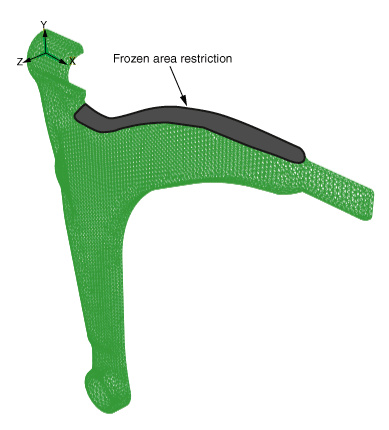
You can apply geometric restrictions to further constrain the topology optimization process to consider only designs that can be manufactured using standard techniques, such as casting or forging. The control arm is manufactured by forging. The demold control geometric restriction shown in Figure 1 ensures that the structure formed by the topology optimization can be removed from the forging die and does not contain undercuts. This example also introduces a frozen area geometric restriction to limit the material that is removed from the upper arm of the structure, as shown in Figure 2.