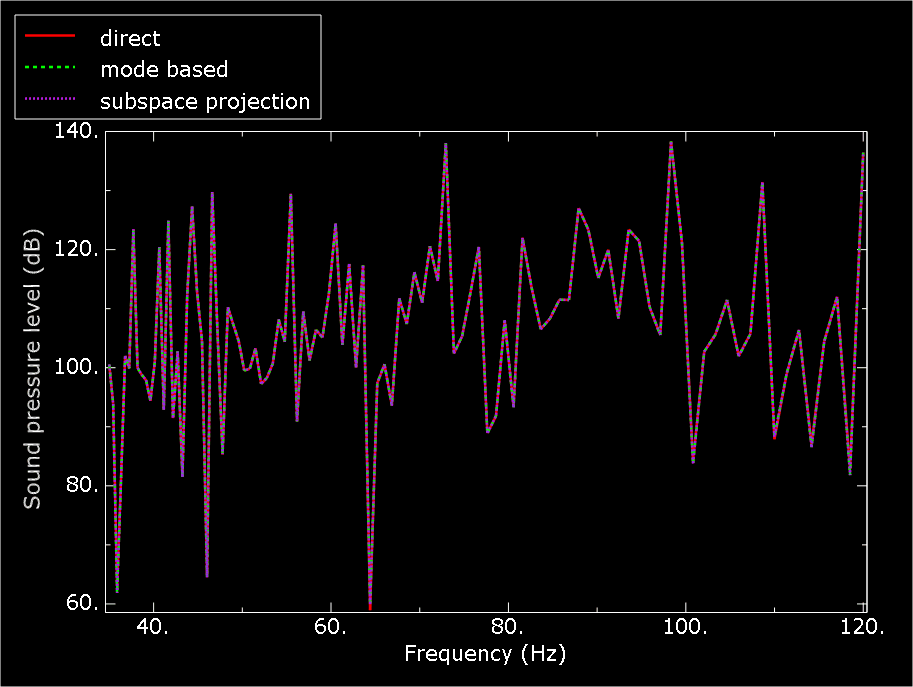
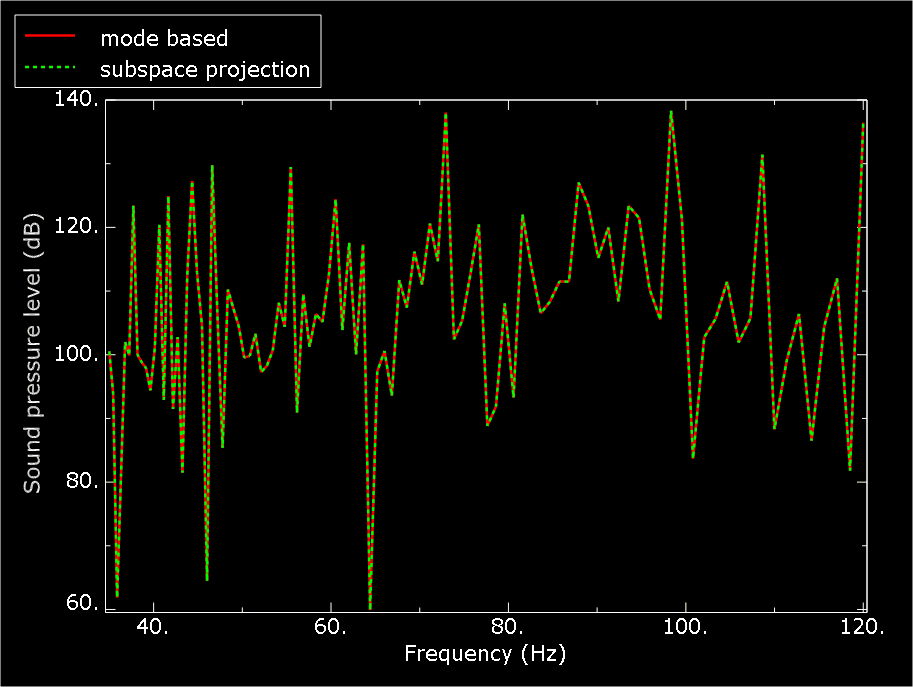
Some of the steady-state dynamic results for the undamped cabin-air model analyses are shown in Figure 4 and Figure 5. In all analyses 200 sampling points are selected in the frequency range of interest (35–120 Hz). This frequency range corresponds to engine-induced vibrations in the range of 2100–7200 RPM. Of particular interest in these analyses is the sound pressure level at a location in the vicinity of the driver's ear. The response is shown in Figure 4 and is calculated from the acoustic pressure using the following equation
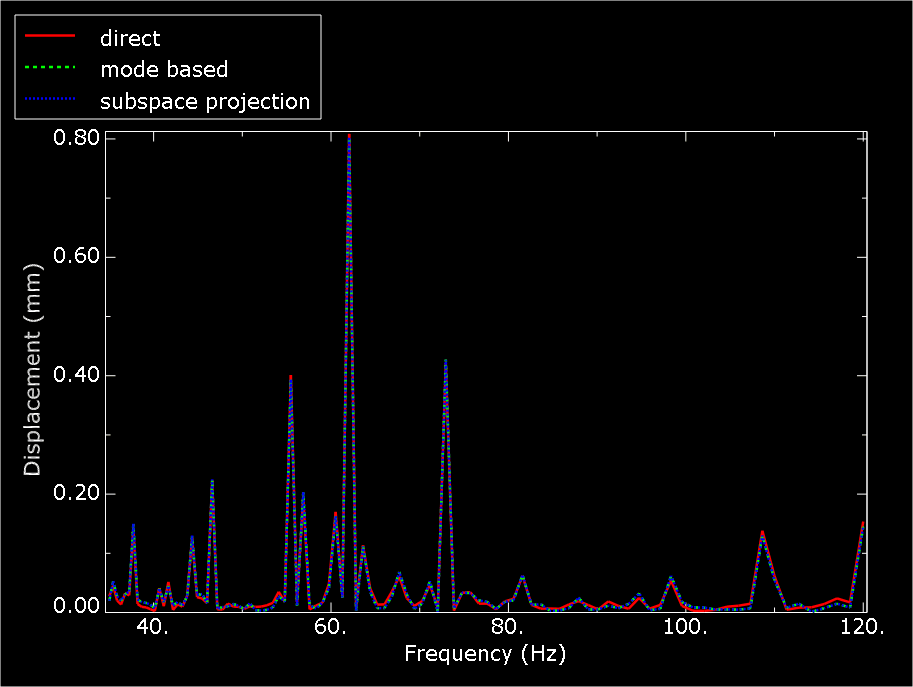
where and Pa. Figure 5 shows the displacement response of one of the nodes on the cabin floor where the harmonic load is applied. The results from the subspace-based and the mode-based steady-state dynamic analyses are virtually identical (as expected), and they compare quite well with the results from the direct steady-state dynamics analysis (Figure 4 and Figure 5). The sound pressure level as computed in these analyses is very high since no damping is considered (neither structural nor impedance-like at the structural-acoustic interface).
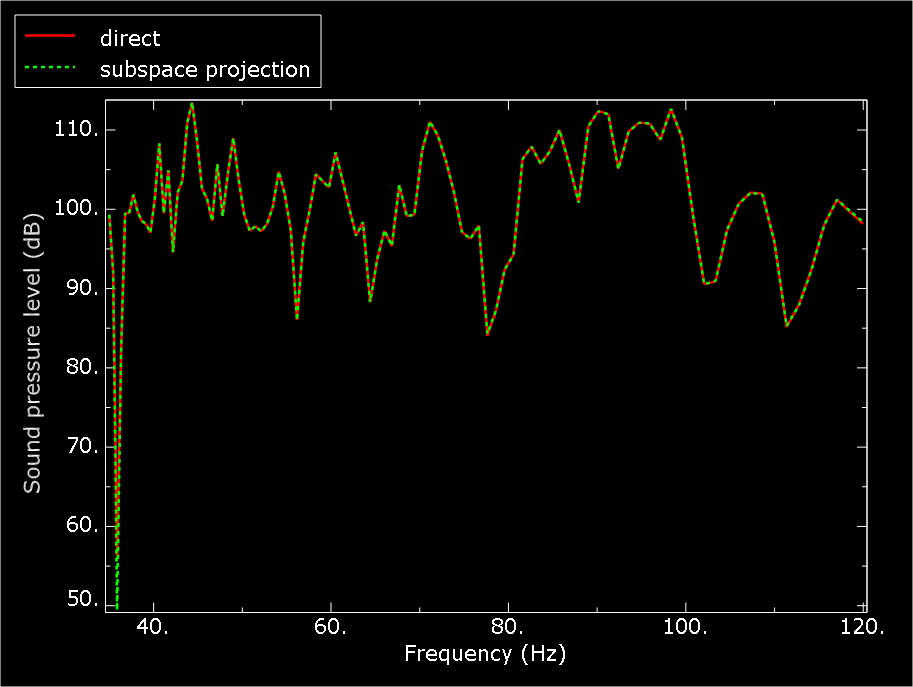
Figure 6 shows the noise level for the cabin-air model when damping is considered. Since the mode-based steady-state dynamics analysis would not take into account the forms of damping considered here, only results from the subspace projection and direct analyses are computed. The results compare quite well. Notably, the subspace projection analysis is approximately 20 times faster than the direct analysis. While the sound pressure level is significantly lower in this analysis when compared to the analysis with no damping, the level is still very high. This suggests that the damping considered in this model is still quite low. Impedance-type damping is considered only on the cabin floor; thus, 100% of the acoustic waves would be reflected from the cabin walls, roof, doors, and windows to produce a higher sound pressure level.
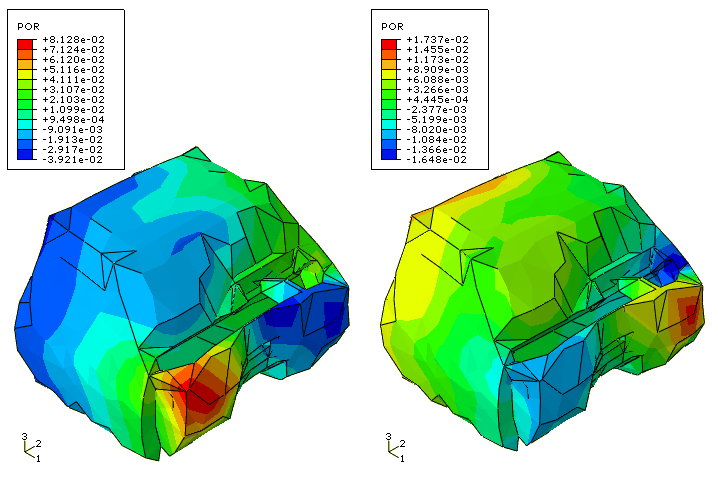
Figure 7 shows the real part of the acoustic pressure in the cabin volume at 120 Hz for both the plane wave (left) and diffuse field (right) excitations. The same damping is used as in the previous case—an impedance defined on the cabin floor. The same source location, a point on the radiator, and the same standoff, a point on the bulkhead, are used for both excitations. These figures illustrate the typical effect of the diffuse excitation option—it produces a more even distribution of pressure in the cabin. This occurs because the incident pressure is divided into many waves, striking the bulkhead from different directions and resulting in a degree of cancellation and averaging of the pressure load on the surface. The results shown are obtained using the direct steady-state dynamics procedure; using the subspace projection steady-state dynamics procedure, the results appear nearly identical.
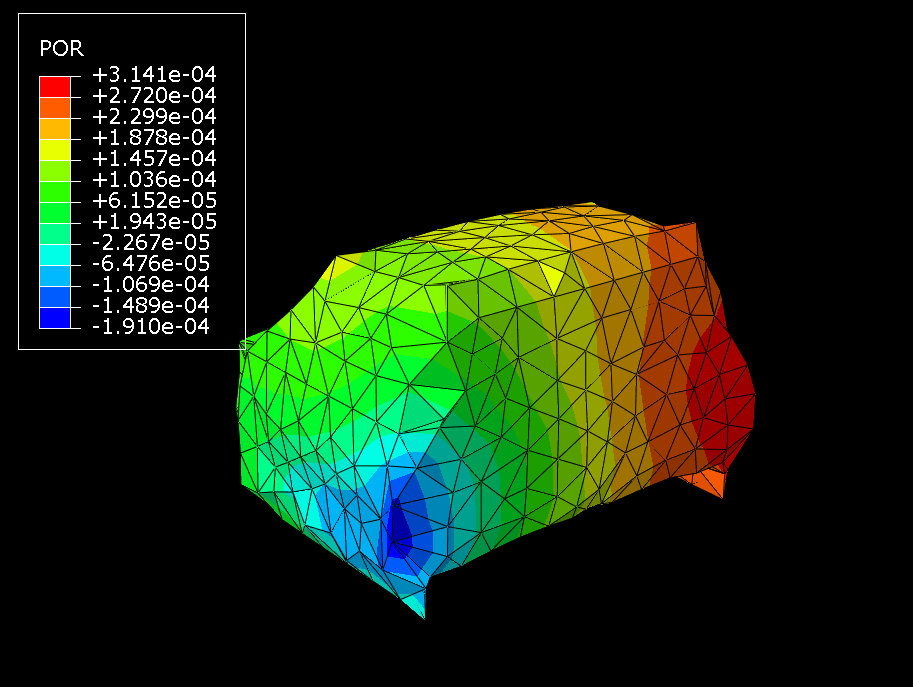
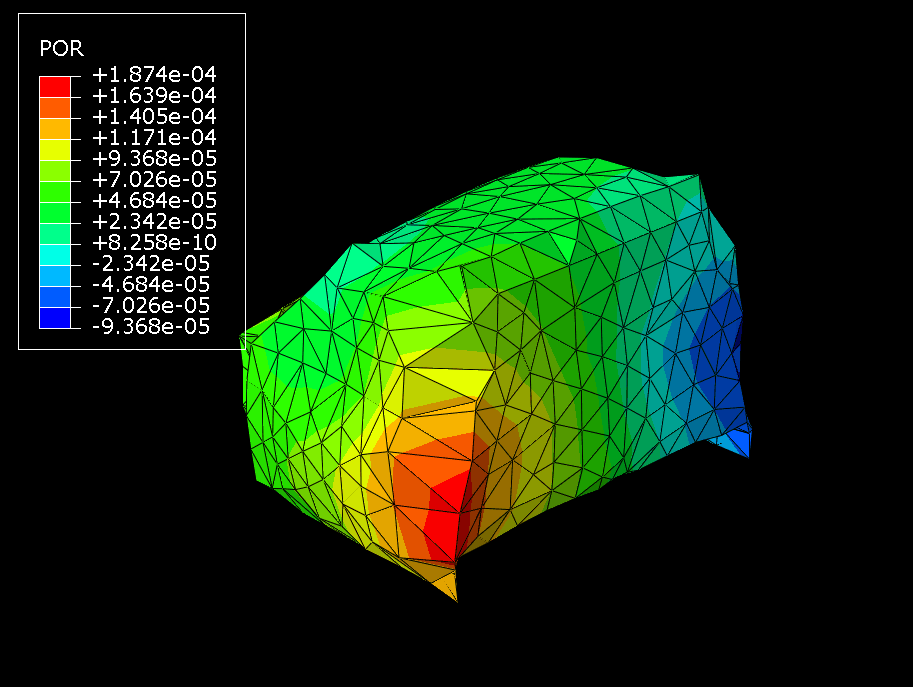
The frequency analysis performed on the cabin-air substructure generates eigenvalues identical to those from the model without substructures. Moreover, the eigenmodes obtained from the regular non-substructure model (Figure 8) and those recovered from the substructure model (Figure 9) compare very well (shown here for the air pressure for the 25th eigenmode).
The frequency response obtained for the cabin-air-chassis model is shown in Figure 10 and Figure 11. Given the size of the model, the direct steady-state dynamics analysis is computationally less efficient and, thus, is not performed. In addition to the natural frequency extraction procedure for the whole structure, a frequency analysis is performed on the equivalent cabin-air-chassis model using two substructures. While the eigenfrequencies are not identical to those obtained from the regular non-substructure model, the differences are quite small for the range of interest, as shown in Figure 12. Once the substructures are generated, the analysis to extract eigenfrequencies from the two-element substructure model is hundreds of times faster than the analysis to extract them from the regular non-substructure model.
The mode-based and the subspace projection steady-state dynamics procedures in Abaqus demonstrate significant improvements in computational efficiency when compared to the direct steady-state dynamics approach. When damping is small or if it can be well approximated using modal damping coefficients, the mode-based procedures are extremely efficient. When damping is more complex, the subspace projection method also demonstrates significant computational advantage in comparison with the direct-integration approach.
The use of substructures is also demonstrated to produce significant gains in computational efficiency. The reduction of the acoustic volume and of its bounding structure to a substructure has clear advantages. The low-dimensional coupled acoustic-structural substructures are very computationally efficient, and the data for the acoustic response inside the substructure can be recovered when the global analysis is completed.