Applying Chebyshev Type I or Type II filtering to an X–Y data object

Use the chebyshev1Filter or chebyshev2Filter function to apply a Chebyshev Type I or Type II filtering operation to a previously saved X–Y data object (a collection of ordered pairs) to produce a new X–Y data object. This filtering operation can be used, for example, to remove high-frequency noise.

See Also
Understanding X–Y data interpolation and extrapolation
Using X–Y data operations
Applying sine-Butterworth filtering to an X–Y data object
Smoothing an X–Y data object
In Other Guides
Filtering Output and Operating on Output in Abaqus/Explicit

Context:

The transfer functions of the Chebyshev filters are shown in Filtering Output and Operating on Output in Abaqus/Explicit.

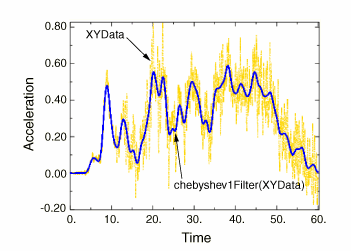
Figure 1 illustrates the type of X–Y plot that can be produced using the chebyshev1Filter operation.

Figure 1. X–Y plot produced using the chebyshev1Filter operation.

The chebyshev1Filter and chebyshev2Filter functions use the same syntax and require the same set of arguments. The following arguments are required: the name of the X–Y data object (name); the cutoff frequency (cutoffFrequency), which is the frequency above which the filter attenuates at least half of the input signal; and the ripple factor (rippleFactor), which is a floating point number that indicates how much oscillation you will allow in exchange for an improved filter response. Both Chebyshev Type I and II filtering require a ripple factor greater than 0; in addition, Chebyshev Type II filtering requires the value to be less than 1. Chebyshev Type I filtering does not place any upper bound on the ripple factor value.

The two types of Chebyshev filters differ in where their response ripples occur and in their handling of the ripple factor value; see Filtering Output and Operating on Output in Abaqus/Explicit for a comparison of Type I and Type II Chebyshev output with typical Butterworth filter output.

A description of the optional arguments follows:

  • The order of the filter you want to use (filterOrder). This argument must be a positive, even integer value; the default value is 2.

  • A symbolic constant specifying the method for computation of the projection and pre-charge to be applied at the start of the data signal (startCondition). Valid values for this argument are ZERO, which applies a constant projection and pre-charge of zero; CONSTANT, which applies a constant projection and pre-charge equal to the first data point in the X–Y data object; MIRROR, which applies a projection and pre-charge equivalent to reflecting the X–Y data object about a vertical line passing through the first data point; REVERSE_MIRROR, which applies a projection and pre-charge equivalent to reflecting the X–Y data object about both a vertical line and a horizontal line passing through the first data point; and TANGENTIAL, which applies a linear projection and pre-charge that is tangential to the first two data points. The default value is CONSTANT.

  • A symbolic constant specifying the method for computation of the projection and pre-charge to be applied at the end of the data signal (endCondition). Valid values for this argument are ZERO, which applies a constant projection and pre-charge of zero; CONSTANT, which applies a constant projection and pre-charge equal to the last data point in the X–Y data object; MIRROR, which applies a projection and pre-charge equivalent to reflecting the X–Y data object about a vertical line passing through the last data point; REVERSE_MIRROR, which applies a projection and pre-charge equivalent to reflecting the X–Y data object about both a vertical line and a horizontal line passing through the last data point; and TANGENTIAL, which applies a linear projection and pre-charge that is tangential to the last two data points. The default value is CONSTANT.

  • A symbolic constant that specifies the interpolation scheme (interpolation). Valid values for this argument are QUADRATIC, specifying a Lagrange second-order interpolation scheme; CUBIC_SPLINE, specifying a cubic spline interpolation scheme; and LINEAR, specifying a linear interpolation scheme. The default value is QUADRATIC.

  • The slope of the raw data curve leading up to the first data point (startslope). This argument's default value is 0.0 (for a level slope), and it is used only when interpolation=CUBIC_SPLINE.

  • The slope of the raw data curve continuing past the final data point (endslope). This argument's default value is 0.0 (for a level slope), and it is used only when interpolation=CUBIC_SPLINE.

  • A Boolean specifying whether a backward pass (backwardPass) is to be performed on the filtered data. The default value for this argument is True. When this argument is set to False, the endCondition argument is ignored.

Your X–Y data object must have a constant time step for it to be filtered. If the time step is not constant, Abaqus/CAE computes additional points at constant intervals by interpolation. The constant time step for Chebyshev Type I or II filtering is defined by the smallest time step in the X–Y data object to be filtered.

  1. Locate the Operate on XY Data dialog box.

    From the main menu bar, select ToolsXY DataCreate. Click Operate on XY data in the dialog box that appears; then click Continue. The Operate on XY Data dialog box appears.

  2. From the Operators listed, click chebyshev1Filter(X,F,F) or chebyshev2Filter(X,F,F) for Chebyshev Type I or Type II filtering, respectively.

    The chebyshev1Filter or chebyshev2Filter function appears in the expression window.

  3. From the XY Data choices, click the name of the X–Y data object on which to operate and click Add to Expression. You can choose from all X–Y data objects previously saved within this session (listed alphabetically in the XY Data field).

    The X–Y data object name appears within the chebyshev1Filter or chebyshev2Filter function parentheses in the expression window.

  4. Position the cursor in the expression window before the second comma, and type in a value for the cutoff frequency.
  5. Position the cursor in the expression window before the third comma, and type in a positive value for the ripple factor. For the chebyshev2Filter function, this value must be less than 1.
  6. To continue to build your expression, position the cursor in the expression window and type in or select the functions, operators, and X–Y data you want to include.
  7. To evaluate and display your expression, click Plot Expression.
  8. To save your new X–Y data object, click Save As and then provide a name in the dialog box that appears.

    Saving your data object makes it available for future operations within this session and for inclusion in X–Y plots containing multiple data objects.

  9. When you are finished, click Cancel to close the dialog box.