Problem description
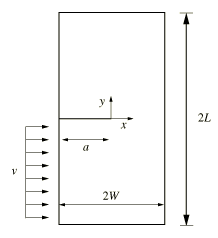
A plate with a single edge crack is studied. The specimen, shown in Figure 1, has dimensions L = 0.003 m and W = 0.0015 m and an initial crack with length a = 0.0015 m. The lower part of the specimen is subjected to an impulse load along the horizontal direction, which is modeled as a prescribed velocity:
where = 25 m/s and = 1.0 × 10–7 s.
The material data for the bulk material properties in the enriched elements are = 3.24 GPa, = 1190 kg/m3, and = 0.35.
The response of cohesive behavior in the enriched elements in the model is specified. The maximum principal stress failure criterion is selected for damage initiation, and an energy-based damage evolution law based on a power law fracture criterion is selected for damage propagation. The relevant material data are as follows: = 100.0 MPa, = 700 N/m, = 700 N/m, = 700 N/m, = 1.0, = 1.0, and = 1.0.