Crack propagation of a single-edge notch simulated using XFEM

This example verifies and illustrates the use of the extended finite element method (XFEM) in Abaqus/Standard to predict crack initiation and propagation of a single-edge notch in a specimen along an arbitrary path by modeling the crack as an enriched feature.

Both the XFEM-based cohesive segments method and the XFEM-based linear elastic fracture mechanics (LEFM) approach are used to analyze this problem. Both two- and three-dimensional models are studied. The specimen is subjected to loadings ranging from pure Mode I to pure Mode II to mixed-mode. In some cases distributed pressure loads are applied to the cracked element surfaces as the crack initiates and propagates in the specimen. The results presented are compared to the available analytical solutions and those obtained using cohesive elements. In addition, the same model is analyzed using the XFEM-based low-cycle fatigue criterion to assess the fatigue life when the model is subjected to sub-critical cyclic loading.

This page discusses:

Problem description
Results and discussion
Input files
Python scripts
References
Figures

ProductsAbaqus/StandardAbaqus/CAE

Problem description

Two single-edge notch specimens are studied. The first specimen is shown in Figure 1 and has a length of 3 m, a thickness of 1 m, a width of 3 m, and an initial crack length of 0.3 m, loaded under pure Mode I loading. Equal and opposite displacements are applied at both ends in the longitudinal direction. The maximum displacement value is set equal to 0.001 m. In the low-cycle fatigue analysis, a cyclic displacement loading with a peak value of 8 × 10⁻⁵ m is specified. The second specimen has a length of 6 m, a thickness of 1 m, a width of 3 m, and an initial crack length of 1.5 m, loaded under pure Mode II or mixed-mode loading. Equal and opposite displacements are applied at both ends in the width direction under pure Mode II loading, while equal and opposite displacements are applied at both ends in both the longitudinal and width directions under mixed-mode loading. The maximum displacement value is set equal to 0.01 m. In the low-cycle fatigue analysis, a cyclic displacement loading with a peak value of 8 × 10⁻⁴ m is specified.

The material data for the bulk material properties in the enriched elements are $E = 210.0$ GPa and $ν = 0.3$ .

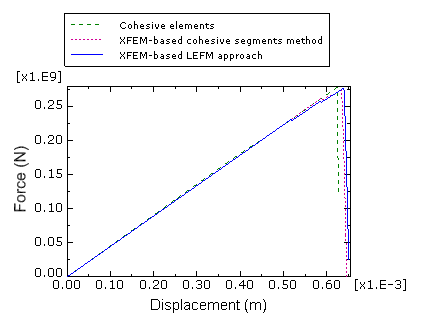
The response of cohesive behavior in the enriched elements in the model is specified. The maximum principal stress failure criterion is selected for damage initiation; and a mixed-mode, energy-based damage evolution law based on a power law criterion is selected for damage propagation. The relevant material data are as follows: $σ_{m a x} = 220$ MPa, $G_{1 C} = 42.2$ × 10³ N/m, $G_{2 C} = 42.2$ × 10³ N/m, $G_{3 C} = $ 42.2× 10³ N/m, and $α = 1.0$ . The relevant material data defined above are also used in the model simulated using the XFEM-based LEFM approach.

When the fatigue crack growth analysis is performed, the additional relevant data for the fracture energy release rate–based Paris law are as follows: $c_{1} = 0.5$ , $c_{2} = - 0.1$ , $c_{3} = 4.88$ × 10⁻⁶, $c_{4} = 1.15$ , $\frac{G_{t h r e s h}}{G_{C}} = 0.001$ , and $\frac{G_{p l}}{G_{C}} = 0.85$ . When the stress intensity factor–based Paris law is used, the equivalent constants are $c_{3} = 4.17$ × 10⁻¹⁹, $c_{4} = 2.3$ .

Results and discussion

Figure 2 shows plots of the prescribed displacement versus the corresponding reaction force obtained using the XFEM method under the pure Mode I loading compared with the results obtained using cohesive elements. The results displayed are from the two-dimensional plane strain analyses. The results obtained using the XFEM method agree well with those obtained using cohesive elements. The results from the equivalent three-dimensional models show similar agreement.

Under the pure Mode II or mixed-mode loading, the crack will no longer propagate along a straight path and will instead propagate along a path based on the maximum tangential stress criterion according to Erdogan and Sih (1963). The direction of crack propagation is given by

\hat{θ} = \cos^{- 1} (\frac{3 K_{I I}^{2} + \sqrt{K_{I}^{4} + 8 K_{I}^{2} K_{I I}^{2}}}{K_{I}^{2} + 9 K_{I I}^{2}}),

where the crack propagation angle, $\hat{θ}$ , is measured with respect to the crack plane. $\hat{θ} = 0$ represents the crack propagation in the “straight-ahead” direction. $\hat{θ} < 0$ if $K_{I I} > 0$ while $\hat{θ} > 0$ if $K_{I I} < 0$ . Under pure Mode II loading, the above equation predicts that the crack will propagate at an angle of 70° while the crack propagation angle predicted using XFEM is 66.5°, which is illustrated in Figure 3.

Input files

Pure Mode I loading

XFEM-based cohesive segments method:

crackprop_mode_I_xfem_cpe4r.inp: Two-dimensional plane strain model with reduced integration.
crackprop_mode_I_xfem_cpe4.inp: Two-dimensional plane strain model.
crackprop_mode_I_xfem_dload_cpe4.inp: Two-dimensional plane strain model with distributed pressure loads.
crackprop_mode_I_xfem_cps4r.inp: Two-dimensional plane stress model with reduced integration.
crackprop_mode_I_xfem_cps4.inp: Two-dimensional plane stress model.
crackprop_mode_I_xfem_dload_cps4.inp: Two-dimensional plane stress model with distributed pressure loads.
crackprop_mode_I_xfem_dload_cax4.inp: Axisymmetric model with distributed pressure loads.
crackprop_mode_I_xfem_c3d4.inp: Three-dimensional tetrahedron model.
crackprop_mode_I_xfem_dload_c3d4.inp: Three-dimensional tetrahedron model with distributed pressure loads.
crackprop_mode_I_xfem_c3d8r.inp: Three-dimensional brick model with reduced integration.
crackprop_mode_I_xfem_c3d8.inp: Three-dimensional brick model.
crackprop_mode_I_xfem_dload_c3d8.inp: Three-dimensional brick model with distributed pressure loads.
crackprop_mode_I_xfem_c3d10.inp: Three-dimensional second-order tetrahedron model.

XFEM-based LEFM approach:

crackprop_mode_I_lefm_xfem_cpe4r.inp: Two-dimensional plane strain model with reduced integration.
crackprop_mode_I_lefm_xfem_cpe4.inp: Two-dimensional plane strain model.
crackprop_mode_I_lefm_xfem_c3d4.inp: Three-dimensional tetrahedron model.
crackprop_mode_I_lefm_xfem_c3d8r.inp: Three-dimensional brick model with reduced integration.
crackprop_mode_I_lefm_xfem_c3d10.inp: Three-dimensional second-order tetrahedron model.

XFEM-based low-cycle fatigue analysis:

crackprop_mode_I_fatigue_xfem_cpe4.inp: Same as crackprop_mode_I_lefm_xfem_cpe4.inp but subjected to cyclic displacement loading.
crackprop_mode_I_fatigue_xfem_c3d8r.inp: Same as crackprop_mode_I_lefm_xfem_c3d8r.inp but subjected to cyclic displacement loading.
crackprop_mode_I_fatigue_xfem_c3d10.inp: Same as crackprop_mode_I_lefm_xfem_c3d10.inp but subjected to cyclic displacement loading.

Pure Mode II loading

XFEM-based cohesive segments method:

crackprop_mode_II_xfem_cpe4r.inp: Two-dimensional plane strain model with reduced integration.
crackprop_mode_II_xfem_cpe4.inp: Two-dimensional plane strain model.
crackprop_mode_II_xfem_cps4r.inp: Two-dimensional plane stress model with reduced integration.
crackprop_mode_II_xfem_cps4.inp: Two-dimensional plane stress model.
crackprop_mode_II_xfem_c3d4.inp: Three-dimensional tetrahedron model.
crackprop_mode_II_xfem_c3d8r.inp: Three-dimensional brick model with reduced integration.
crackprop_mode_II_xfem_c3d8.inp: Three-dimensional brick model.
crackprop_mode_II_xfem_c3d8r_user.inp: Same as crackprop_mode_II_xfem_c3d8r.inp but with user-defined damage initiation criterion.
crackprop_maxps_xfem_udmgini.f: Subroutine for user-defined damage initiation criterion.
crackprop_mode_II_xfem_c3d10.inp: Three-dimensional second-order tetrahedron model.

XFEM-based LEFM approach:

crackprop_mode_II_lefm_xfem_cpe4r.inp: Two-dimensional plane strain model with reduced integration.
crackprop_mode_II_lefm_xfem_cpe4.inp: Two-dimensional plane strain model.
crackprop_mode_II_lefm_xfem_c3d4.inp: Three-dimensional tetrahedron model.
crackprop_mode_II_lefm_xfem_c3d8r.inp: Three-dimensional brick model with reduced integration.
crackprop_mode_II_lefm_xfem_c3d10.inp: Three-dimensional second-order tetrahedron model.

XFEM-based low-cycle fatigue analysis:

crackprop_mode_II_fatigue_xfem_cpe4.inp: Same as crackprop_mode_II_lefm_xfem_cpe4.inp but subjected to cyclic displacement loading.
crackprop_mode_II_fatigue_xfem_c3d8r.inp: Same as crackprop_mode_II_lefm_xfem_c3d8r.inp but subjected to cyclic displacement loading using the direct cyclic approach.
crackprop_mode_II_fatigue_xfem_c3d8r_2.inp: Same as crackprop_mode_II_lefm_xfem_c3d8r.inp but subjected to cyclic displacement loading using the general fatigue crack growth approach.
crackprop_mode_II_fatigue_xfem_c3d8r_2_simp.inp: Same as crackprop_mode_II_lefm_xfem_c3d8r.inp but subjected to cyclic displacement loading using the simplified fatigue crack growth approach.
crackprop_mode_II_fatigue_xfem_c3d8r_3_tabular.inp: Same as crackprop_mode_II_fatigue_xfem_c3d8r_2.inp but with the tabular form to define fatigue crack growth.
crackprop_mode_II_fatigue_xfem_c3d8r_3_user.inp: Same as crackprop_mode_II_fatigue_xfem_c3d8r_2.inp but with the user-defined subroutine to define fatigue crack growth.
crackprop_mode_II_fatigue_xfem_c3d8r_3_simp_tabular.inp: Same as crackprop_mode_II_fatigue_xfem_c3d8r_2_simp.inp but with the tabular form to define fatigue crack growth.
crackprop_mode_II_fatigue_xfem_c3d8r_3_simp_user.inp: Same as crackprop_mode_II_fatigue_xfem_c3d8r_2_simp.inp but with the user-defined subroutine to define fatigue crack growth.
crackprop_mode_II_fatigue_xfem_c3d10.inp: Same as crackprop_mode_II_lefm_xfem_c3d10.inp but subjected to cyclic displacement loading.
crackprop_mode_II_fatigue_xfem_c3d10_2.inp: Same as crackprop_mode_II_lefm_xfem_c3d10.inp but subjected to cyclic displacement loading using the general fatigue crack growth approach.
crackprop_mode_II_fatigue_xfem_c3d10_2_irwin.inp: Same as crackprop_mode_II_fatigue_xfem_c3d10_2.inp but with the IRWIN law to define fatigue crack growth.
crackprop_mode_II_fatigue_xfem_c3d10_2_tabular_kbased.inp: Same as crackprop_mode_II_fatigue_xfem_c3d10_2.inp but with the K-BASED tabular form to define fatigue crack growth.
crackprop_mode_II_fatigue_xfem_c3d10_2_user_kbased.inp: Same as crackprop_mode_II_fatigue_xfem_c3d10_2.inp but with the K-BASED user-defined subroutine to define fatigue crack growth.
crackprop_fatigue_3d_3_user.f: User subroutine UMIXMODEFATIGUE used in crackprop_mode_II_fatigue_xfem_c3d8r_3_user.inp and crackprop_mode_II_fatigue_xfem_c3d8r_3_simp_user.inp.
crackprop_fatigue_3d_3_kbased_user.f: User subroutine UMIXMODEFATIGUE used in crackprop_mode_II_fatigue_xfem_c3d10_2_user_kbased.inp.

Mixed-mode loading

XFEM-based cohesive segments method:

crackprop_mixmode_xfem_cpe4r.inp: Two-dimensional plane strain model with reduced integration.
crackprop_mixmode_xfem_cpe4.inp: Two-dimensional plane strain model.
crackprop_mixmode_xfem_cps4r.inp: Two-dimensional plane stress model with reduced integration.
crackprop_mixmode_xfem_cps4.inp: Two-dimensional plane stress model.
crackprop_mixmode_xfem_c3d4.inp: Three-dimensional tetrahedron model.
crackprop_mixmode_xfem_c3d8r.inp: Three-dimensional brick model with reduced integration.
crackprop_mixmode_xfem_c3d8.inp: Three-dimensional brick model.
crackprop_mixmode_xfem_c3d10.inp: Three-dimensional second-order tetrahedron model.

Python scripts

Pure Mode II loading

XFEM-based LEFM approach:

crackprop_mode_II_lefm_xfem_cpe4.py: Script to generate the two-dimensional plane strain model in Abaqus/CAE.
crackprop_mode_II_lefm_xfem_c3d8r.py: Script to generate the three-dimensional brick model in Abaqus/CAE.

Mixed-mode loading

XFEM-based cohesive segments method:

crackprop_mixmode_xfem_cpe4.py: Script to generate the two-dimensional plane strain model in Abaqus/CAE.
crackprop_mixmode_xfem_c3d8.py: Script to generate the three-dimensional brick model in Abaqus/CAE.

References

Erdogan, F., and G. C. Sih, “On the Crack Extension in Plates under Plane Loading and Transverse Shear,” Journal of Basic Engineering, vol. 85 519–527, 1963.

Figures