Acoustic radiation impedance of a sphere in breathing mode

A spherical cavity of unit radius in an unbounded acoustic medium is subjected to a uniform radial velocity on its inner surface. The analytical solution for the acoustic pressure is of the form

where $p$ is the acoustic pressure, ${\rho }_f$ is the fluid density, $c_f=\sqrt{K_f/{\rho }_f}$ is the speed of sound, $K_f$ is the bulk modulus, $k=2\pi f/c_f$ is the acoustic wave number, $f$ is the frequency, $r$ is the radial coordinate, $\mathbf{n}$ is the normal unit vector pointing into the fluid, and $v_n=-{\dot{\mathbf{u}}}^f\cdot \mathbf{n}$ is the prescribed inward particle velocity on the spherical boundary. The ratio of the pressure to the velocity on the boundary is called the acoustic impedance (see Junger and Feit, 1972); for the zeroth (breathing) mode the impedance is given by

The imaginary part of the impedance is given by

where

is the magnitude of the impedance.

The absorbing boundary condition used here is the first-order condition of Bayliss, Gunzberger, and Turkel (1982):

where $r_1$ is the radius of the spherical truncation boundary of the finite element mesh. This boundary condition is theoretically exact for all vibration frequencies in the breathing mode. Since conservation of linear momentum requires

and the impedance enforces the condition

the first-order Bayliss et al. boundary condition can be enforced in the steady-state dynamic procedure by specifying impedance parameters given by

and

In Abaqus this spherical radiation impedance can also be defined by specifying the radius of the terminating spherical mesh boundary.

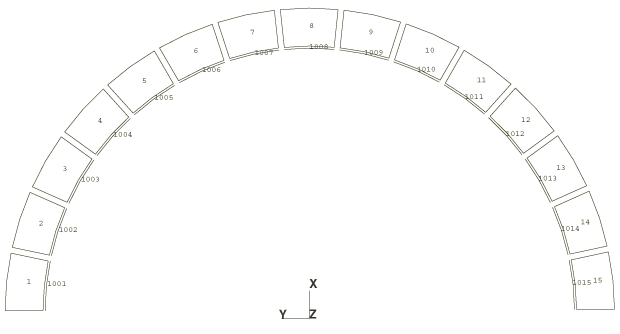
Figure 1 shows the finite element mesh using a single layer of 15 ACAX8 elements, with ASI3A coupling elements on the inner surface and the impedance applied to the outer faces of the ACAX8 elements. Uniform radial velocities are applied to the inner surface transforming the spherical coordinates to a local coordinate system before specifying the magnitudes. The dimensions and acoustic properties of this problem are chosen to facilitate comparison with the analytical value of the impedance, $Z_0$ With ${\rho }_f=1$ and $K_f=4{\pi }^2$, $c_f=2\pi$, and the acoustic wave number $k=2\pi f/c_f$ is equal to the analysis frequency in Hertz, $f.$ Moreover, if the imposed normal velocity $v_n=1/2\pi$, the value of the pressure variable on the inner boundary will equal the value for the impedance, $Z_0$. This normal velocity is imposed using a boundary condition in conjunction with a transformed coordinate system, as shown in acousticimpsphere_acax8_bayliss.inp. Since the degrees of freedom representing the tangential velocity components have no stiffness associated with them, they must be constrained to prevent solver problems.

The outer boundary is placed at $r_1=1+1/2\pi$ to provide a good aspect ratio for the elements; its value has no other significance for this problem. For comparison, the same mesh was reanalyzed using the default plane wave absorbing condition. This plane wave absorber is equal to the limiting value of the Bayliss et al. first-order condition as $r_1\to \mathrm{\infty }$ and is theoretically exact for absorption of planar wavefronts normally incident on a planar truncation boundary.

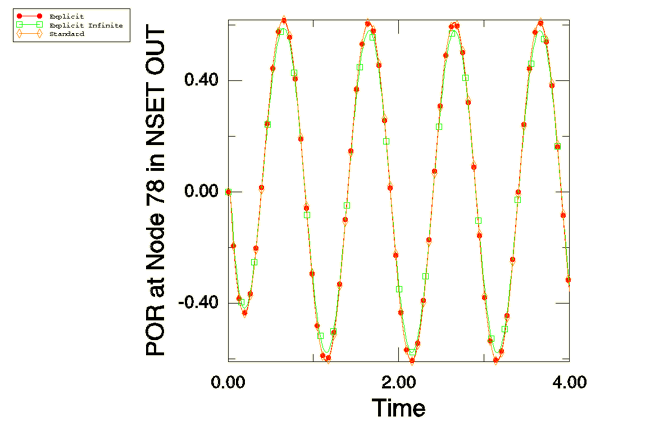
A steady-state dynamic analysis is performed in Abaqus/Standard over a range of frequencies from 0 to 20 Hz. The transient simulations are also performed in Abaqus/Explicit with an excitation frequency of 1 Hz. Different excitation frequencies can be tested by changing the parameters defined in the input files.

The steady-state analysis was also performed in Abaqus/Standard using three-dimensional and axisymmetric acoustic infinite elements. These acoustic infinite elements use infinite-direction basis functions that are based on radiating modes of a sphere (see Acoustic infinite elements). Consequently, the impedance for the spherical breathing mode is modeled accurately by these elements, and the results obtained using acoustic infinite elements should closely match the results obtained using spherical radiation impedance conditions. However, for more complex wave shapes the acoustic infinite elements are expected to give more accurate results, owing to the richness of the basis functions used to model the variation of the acoustic field in the infinite direction. The infinite element mesh required to model this problem consists only of acoustic infinite elements on the spherical surface, with acoustic-structural interface elements added (with the same mesh topology) to facilitate imposition of the velocity boundary condition at the surface of the sphere. The reference point for the infinite elements is located at the center of the sphere. For this problem a single input file, acousticimpsphere_acin.inp, includes sections of the sphere modeled with each of the three-dimensional acoustic infinite elements: ACIN3D3, ACIN3D4, ACIN3D6, and ACIN3D8. Two additional input files, acousticimpsphere_acinax2.inp and acousticimpsphere_acinax3.inp, model the problem using semicircular meshes of ACINAX2 and ACINAX3 elements, respectively.

For the transient analyses in Abaqus/Explicit the Bayliss et al. boundary condition is enforced using spherical radiation impedance conditions. On the inner radius of the mesh the shell elements in the three-dimensional case and beam elements in the axisymmetric case are connected to the acoustic domain with a tie constraint. The transient analysis is also performed in Abaqus/Explicit using three-dimensional and axisymmetric acoustic infinite elements instead of defining the impedance. Two additional input files, acousticimpsphere_acin3d4_xpl.inp and acousticimpsphere_acinax2_xpl.inp, model the three-dimensional and axisymmetric problems, respectively.