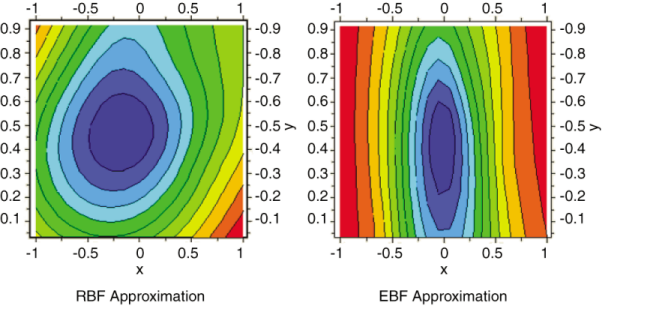
Overview
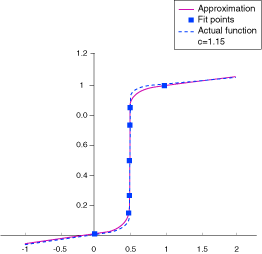
Radial Basis Functions (RBF) are a type of neural network employing a hidden layer of radial units and an output layer of linear units. Elliptical Basis Functions (EBF) are similar to Radial Basis Functions but use elliptical units in place of radial units. Compared to RBF networks where all inputs are handled equally, EBF networks treat each input separately using individual weights.
RBF networks are characterized by reasonably fast training and reasonably compact networks. On the other hand, EBF networks require more iterations to learn individual input weights and are often more accurate than RBFs.
Weissinger (1947) was the first to use numeric potential flow to calculate the flow around wings. The potential flow equations are a radial basis function. Hardy (1971) realized that the same concept could be used to fit geophysical data to geophysical phenomena. Broomhead and Lowe (1988) renamed this technology “neural nets,” and it was subsequently used to approximate all types of behavior.
An advantage of choosing EBF over RBF is EBF’s ability to rank the input variables in the order of influence on the output variables as described in Ranking the Influence of Input Variables on Output Variables.