Multiscale materials

Linear elastic composites

Elements tested

C3D8R

Features tested

Linear elastic multiscale materials modeled with mean-field homogenization methods.

Problem description

The verification tests consist of a set of single-element tests that use C3D8R elements under mechanical and thermal loading conditions. All constituents of the composite material are linear elastic. Material properties including Young's modulus, $E,$ and Poisson's ratio, $ν,$ are listed below. Microstructure properties including volume fraction, $v_{f},$ and aspect ratio, $a_{r},$ are also listed.

Material:

Composite 1

Matrix properties:


$E$	250 GPa
$ν$	0.3
$v_{f}$	80%

Inclusion one properties:


$E$	750 GPa
$ν$	0.3
$v_{f}$	10%
$a_{r}$	infinite

Inclusion two properties:


$E$	1000 GPa
$ν$	0.3
$v_{f}$	10%
$a_{r}$	infinite

Both inclusions are cylindrical and aligned.

Composite 2

Matrix properties:


$E$	3.16 GPa
$ν$	0.35

Inclusion properties:


$E$	73.1 GPa
$ν$	0.18
$a_{r}$	1.0

The inclusions are spherical with variable volume fractions.

Composite 3

Matrix properties:


$E$	70 GPa
$ν$	0.33

Inclusion properties:


$E$	300 GPa
$ν$	0.2
$v_{f}$	10%
$a_{r}$	20.0

The shape of the inclusion is prolate, and the inclusions are aligned.

Composite 4

Matrix properties:


$E$	4.5 GPa
$ν$	0.38

Inclusion properties:


$E$	172 GPa
$ν$	0.2
$a_{r}$	0.04

The inclusion is penny-shaped and randomly oriented in 3D.

Composite 5

The material properties are the same as those for Composite 4, but the inclusion directions are specified with a different second-order orientation tensor,

a = [\begin{matrix} 0.515 & - 0.038 & - 0.059 \\ - 0.038 & 0.375 & - 0.063 \\ - 0.059 & - 0.063 & 0.11 \end{matrix}] .

Composite 6

Matrix properties:


$E$	3 GPa
$ν$	0.35
CTE	70e-6 $K^{- 1}$

Inclusion properties:


$E$	172 GPa
$ν$	0.2
CTE	1e-6 $K^{- 1}$

The volume fraction and aspect ratio of the inclusion are variable.

Composite 7

Matrix properties:


$E$	3.45 GPa
$ν$	0.35

Inclusion properties:


$E$	73.1GPa
$ν$	0.22

The inclusion is continuous fiber (cylinder-shaped).

Composite 8

Matrix properties:


$E$	5.35 GPa
$ν$	0.354

Inclusion properties (transversely isotropic):


$E_{1}$	232 GPa
$E_{2}$	15 GPa
$ν_{12}$	0.279
$ν_{23}$	0.49
$G_{12}$	24 GPa

The inclusion is continuous fiber (cylinder-shaped).

Results and discussion

A two-step mean-field homogenization method is used to obtain the transverse response of Composite 1. Both Mori-Tanaka and the balanced homogenization model are used in Step 1, and Voigt homogenization is used in Step 2. Results are compared with the FE-RVE prediction in Table 1. The mean-field predictions show good agreement with the FE-RVE results.

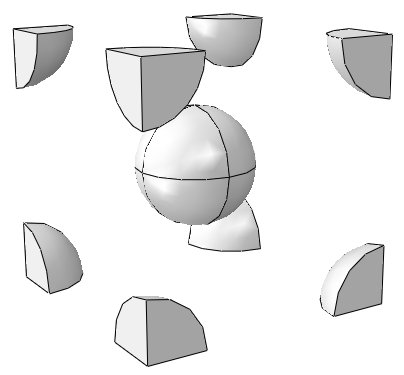
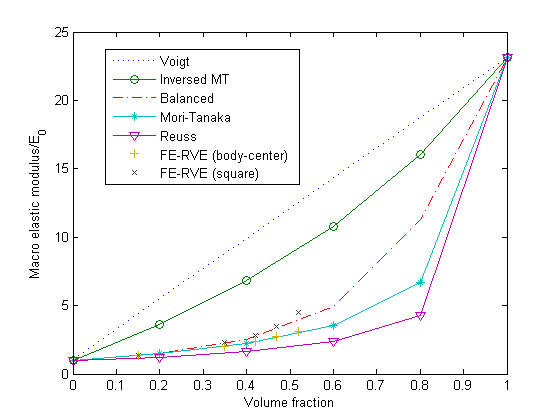
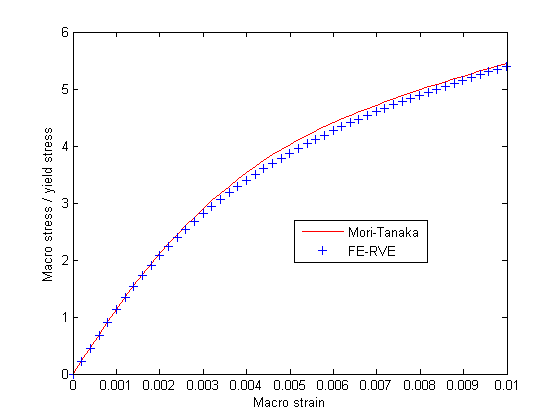
The influence of the volume fraction on the normalized macroscale modulus of Composite 2 is plotted in Figure 2 using various homogenization methods. Two different FE-RVEs are used for comparison: body-centered and square packed. The body-centered FE-RVE is shown in Figure 1. The square-packed FE-RVE is also a cubic cell with only a single sphere in the middle of the cell. The Mori-Tanaka prediction matches the body-centered FE-RVE prediction very well, while the balanced prediction matches the square-packed FE-RVE results very well up to a volume fraction of 50%. Interaction between inclusions is stronger in the squared-packed FE-RVE compared to the body-centered FE-RVE, which can be better captured with the balanced method.

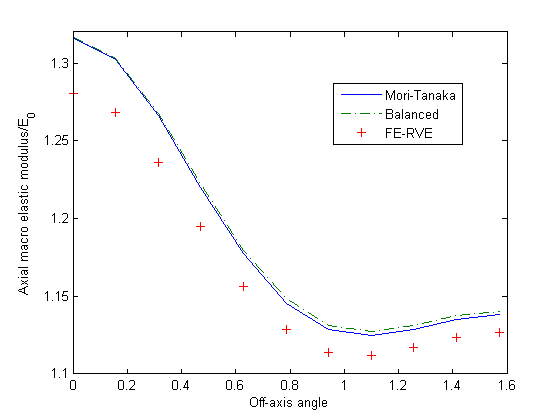
Composites with various off-axis angles are tested with Composite 3. The influence of the off-axis angle on the normalized macroscale modulus in the traction direction is plotted in Figure 3. Mori-Tanaka and the balanced homogenization methods are used, and the predicted macroscale properties compare well with the FE-RVE results. The body-centered FE-RVE model is used to obtain the stiffness modulus of the composite through a linear perturbation step as described above. The engineering constants predicted by the FE-RVE model are listed in Table 2, with the 1-direction being the inclusion direction. The axial macroscale elastic modulus is then computed at all off-axis angles through transformation.

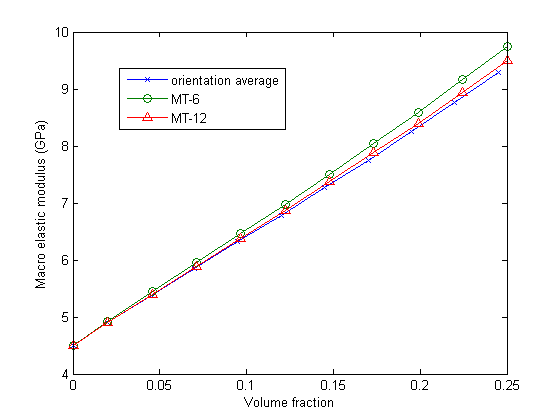
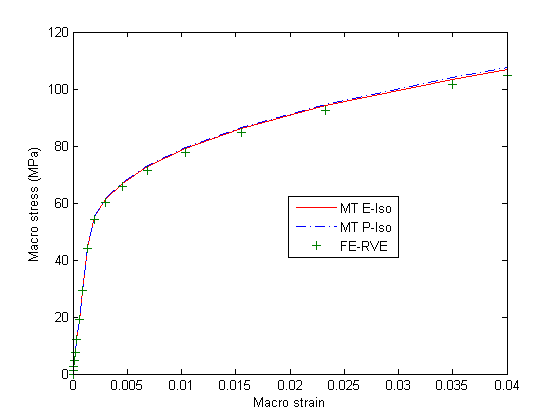
The influence of the volume fraction on the macroscale elastic modulus of Composite 4 in the traction direction is plotted in Figure 4. 6 × 6 angle subdivisions and 12 × 12 angle subdivisions are used for the numerical integration over the orientations. Two-step homogenization is used; Mori-Tanaka homogenization is used in Step 1, and Voigt homogenization is used in Step 2. For comparison, the macroscale elastic modulus is also computed directly using the orientation average,

\begin{array}{l} C_{i j k l}^{} & = & ​ C_{1} a_{i j k l} + C_{2} (a_{i j} δ_{k l} + a_{k l} δ_{i j}) + C_{3} (a_{i k} δ_{j l} + a_{i l} δ_{j k} + a_{j l} δ_{i k} + a_{j k} δ_{i l}) \\ ​ & + & C_{4} δ_{i j} δ_{k l} + C_{5} (δ_{i k} δ_{j l} + δ_{i l} δ_{j k}), \end{array}

where

C_{i}^{'} s

are the five constants of a transversely orthotropic material and

C_{i j k l}^{U D}

are the components of the elastic modulus of the transversely orthotropic material with symmetry around axis-1:

C_{1} = C_{1111}^{U D} - 2 C_{1133}^{U D} {+ C}_{3322}^{U D} - 4 C_{1313}^{U D}_{}^{} + 2 C_{2323}^{U D}

C_{2} = C_{1133}^{U D} - C_{3322}^{U D}

C_{3} = C_{1313}^{U D} - C_{2323}^{U D}

C_{4} = C_{3322}^{U D}

C_{5} = C_{2323}^{U D} .

a_{i j}

is the second-order orientation tensor, which is

a = [\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix}]

for 3D randomly distributed orientations. The fourth-order orientation tensor is computed using

a_{i j k l} = \iint p_{i} p_{j} p_{k} p_{l} Ψ (θ, φ) \sin θ d θ d φ,

where

p = [\sin θ \cos φ, \sin θ \sin φ, \cos θ]

is the fiber direction and

Ψ

is the orientation distribution function.

The same studies are made with Composite 5, and the results are plotted in Figure 5. The predicted macroscale modulus matches well with the orientation average.

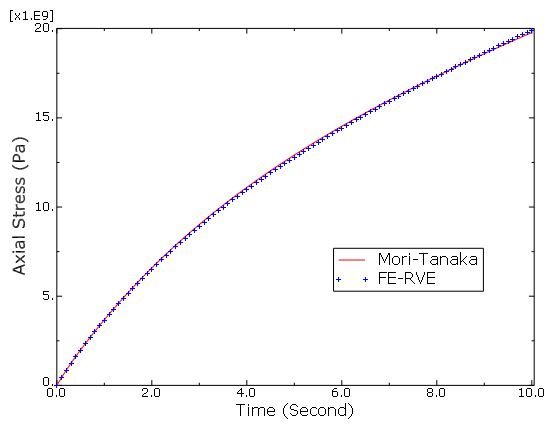
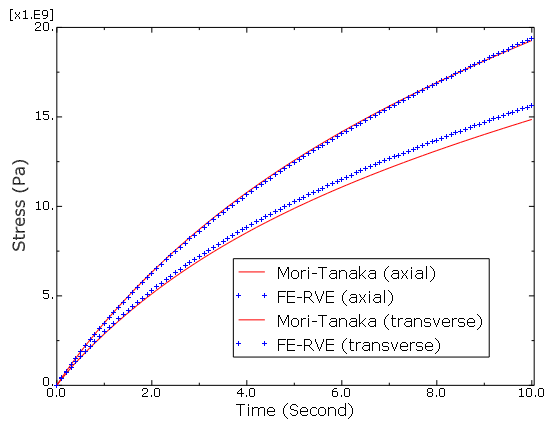
Thermal-elastic composites under thermal loading are also tested with Composite 6. The influence of aspect ratio on the predicted macroscale coefficient of thermal expansion (CTE) is plotted in Figure 6.

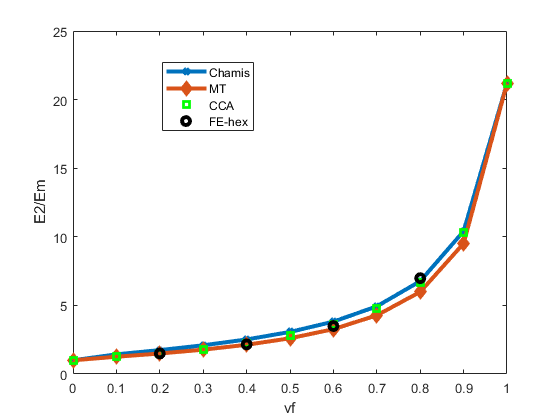
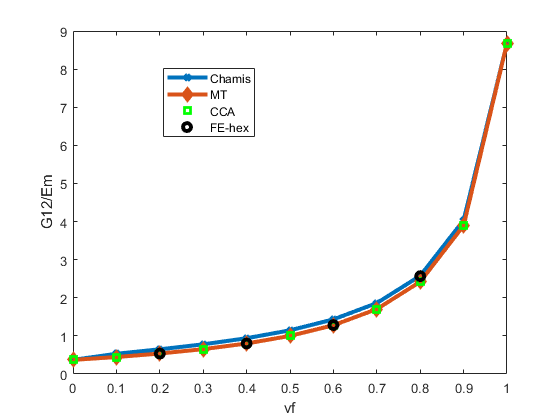
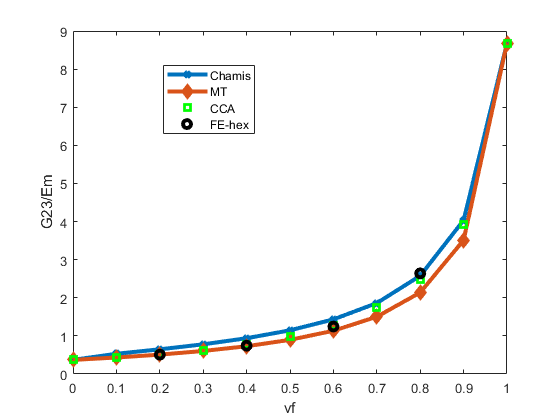
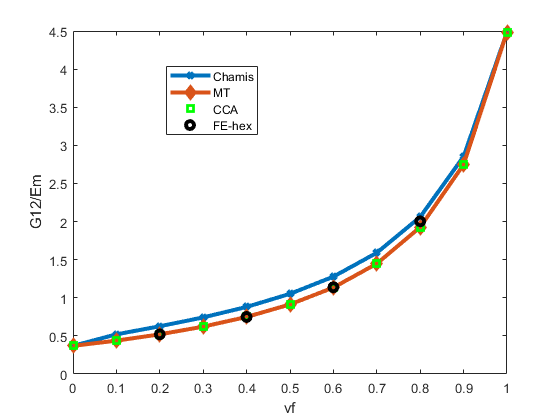
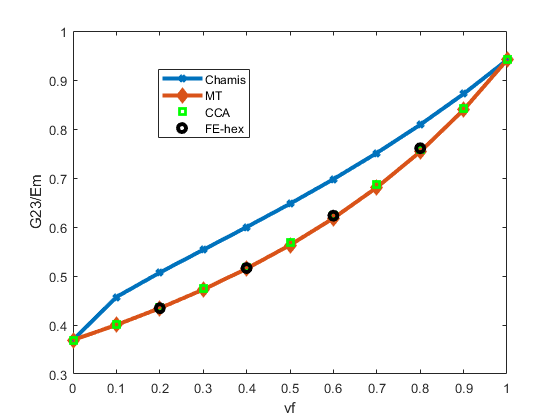
A comparison of homogenized elastic constants is performed for Composites 7 and 8. Both are UD composites with continuous fibers. The fiber material in Composite 7 is isotropic glass fiber, and the fiber material in Composite 8 is transversely isotropic carbon fiber. The homogenized elastic properties are transversely isotropic, and the 1-direction is the fiber direction, which is also the 1-direction of the local direction of the fiber. We compared the homogenized elastic constants computed using Chamis, CCA and Mori-Tanaka formulations with FE-RVE results at various volume fractions. The fibers in the FE-RVEs are hex packed, as shown in Figure 7. The homogenized constants $E_{1}$ and $ν_{12}$ are very close between all results. Therefore, only $E_{2}$ and $G_{12}$ and $G_{23}$ are shown in the figures. Results for epoxy-glass Composite 7 are shown in Figure 8, Figure 9 and Figure 10. We can see that the homogenized results compare well with FE-RVE results, with Chamis and CCA slightly better than Mori-Tanaka at high volume fractions. Results for epoxy-carbon Composite 8 are shown in Figure 11, Figure 12 and Figure 13. The results based on Chamis formulation show the largest deviation compared to FE-RVE results, while both CCA and Mori-Tanaka compare well with FE-RVE results for all volume fractions.

Input files

multscale-twostep-mt.inp: One-element test using Composite 1 with two-step mean-field homogenization. Mori-Tanaka homogenization is used in the first step, and Voigt homogenization is used in the second step.
multscale-twostep-balanced.inp: One-element uniaxial tension test using Composite 1. Traction is applied in the transverse direction. Two-step mean-field homogenization is used. Balanced homogenization is used in the first step, and Voigt homogenization is used in the second step.
multscale-onestep.inp: One-element uniaxial tension test using Composite 1. Traction is applied in the transverse direction. Direct Mori-Tanaka homogenization is used, which is equivalent to using Mori-Tanaka homogenization in both the first and second step.
rve-twocylinder.inp: FE-RVE model of Composite 1 under transverse loading.
multscale-sphere-vf.inp: One-element uniaxial tension tests using Composite 2 with various volume fractions and homogenization methods.
multscale-sphere-vf2.inp: One-element uniaxial tension tests using Composite 2 with various volume fractions and homogenization methods.
rve-sphere-vf10-bc.inp: FE-RVE model of Composite 2 with a volume fraction of 10% under uniaxial tension loading. Inclusions are packed with a body-centered pattern.
rve-sphere-vf10-sq.inp: FE-RVE model of Composite 2 with a volume fraction of 10% under uniaxial tension loading. Inclusions are packed with a square pattern.
multscale-angle-mt.inp: One-element uniaxial tension tests using Composite 3 with various off-axis angles specified with fixed inclusion directions. Mori-Tanaka homogenization is used.
multscale-angle-balanced.inp: One-element uniaxial tension tests using Composite 3 with various off-axis angles specified with fixed inclusion directions. Balanced homogenization is used.
rve-prolate-vf10.inp: FE-RVE model of Composite 3 under uniaxial tension loading. Inclusions are packed with a body-centered pattern and aligned in the direction of the traction.
multscale-penny-random3d-6.inp: One-element uniaxial tension test using Composite 4. Mori-Tanaka homogenization is used; 6 × 6 angle divisions are used for numerical integration.
multscale-penny-random3d-12.inp: One-element uniaxial tension test using Composite 4. Mori-Tanaka homogenization is used; 12 × 12 angle divisions are used for numerical integration.
multscale-penny-oritens-6.inp: One-element uniaxial tension test using Composite 5 with dispersed inclusion orientations specified with a second-order orientation tensor. Mori-Tanaka homogenization is used; 6 × 6 angle divisions are used for numerical integration.
multscale-penny-oritens-12.inp: One-element uniaxial tension test using Composite 5 with dispersed inclusion orientations specified with a second-order orientation tensor. Mori-Tanaka homogenization is used; 12 × 12 angle divisions are used for numerical integration.
multscale-cte-vf2.inp: One-element tests using Composite 6 under thermal loading. Various aspect ratios are used for the inclusions. Mori-Tanaka homogenization is used. The volume fraction of the inclusion is 2%.
multscale-cte-vf5.inp: One-element tests using Composite 6 under thermal loading. Various aspect ratios are used for the inclusions. Mori-Tanaka homogenization is used. The volume fraction of the inclusion is 5%.
multscale-cte-vf10.inp: One-element tests using Composite 6 under thermal loading. Various aspect ratios are used for the inclusions. Mori-Tanaka homogenization is used. The volume fraction of the inclusion is 10%.

References

Pierard, O., C. Friebel, and I. Doghri, “Mean-Field Homogenization of Multi-Phase Thermo-Elastic Composites: a General Framework and its Validation,” Composites Science and Technology, vol. 64, pp. 1587–1603, 2004.
Advani, S., and C. Tucker, “The Use of Tensors to Describe and Predict Fiber Orientation in Short Fiber Composites,” Journal of Rheology, vol. 31(8), pp. 751–784, 1987.
Onat, E. T., and F. A. Leckie, “Representation of Mechanical Behavior in the Presence of Changing Internal Structure,” Journal of Applied Mechanics, vol. 55(1), pp. 1–10, 1988.

Tables

Table 1. Comparison of normalized macroscale transverse elastic modulus with different homogenization methods. Prediction is compared with FE-RVE results.
Method	Mori-Tanaka/Voigt	Balanced/Voigt	Mori-Tanaka/Mori-Tanaka	FE-RVE
$\bar{E_{T}} / E_{0}$	1.2340	1.2408	1.2340	1.2412

Table 2. Normalized macroscale properties of a body-centered FE-RVE with prolate inclusions. The elastic moduli are normalized with the Young's modulus of the matrix constituent $E_{0}$ .
$E_{1}$	$E_{2}$	$E_{3}$	$ν_{12}$	$ν_{13}$	$ν_{23}$	$G_{12}$	$G_{13}$	$G_{23}$
1.28	1.130	1.13	0.316	0.316	0.347	0.421	0.421	0.417

Figures

Linear elastic composites with viscoelasticity

Elements tested

C3D8R

Features tested

Linear elastic composites with viscoelasticity modeled with mean-field homogenization methods.

Problem description

The verification tests consist of a set of single-element tests that use C3D8R elements under uniaxial tension loading conditions. Transient static responses are predicted.

Material:

Composite 1

Matrix properties:


$E$	70 GPa
$ν$	0.33

Prony series coefficients (N=2): ${\bar{g}}_{1}^{P} = 0.55$ , ${\bar{k}}_{1}^{P} = 0$ , $τ_{1} = 1.766$ , ${\bar{g}}_{2}^{P} = 0.4$ , ${\bar{k}}_{2}^{P} = 0$ , $τ_{2} = 0.1536$

Inclusion properties:


$E$	300 GPa
$ν$	0.2
$v_{f}$	0.1
$a_{r}$	20.0

The inclusion shape is prolate, and the directions are aligned.

Composite 2

Matrix properties:


$E$	70 GPa
$ν$	0.33

Prony series coefficients (N=2): ${\bar{g}}_{1}^{P} = 0.55$ , ${\bar{k}}_{1}^{P} = 0$ , $τ_{1} = 1.766$ , ${\bar{g}}_{2}^{P} = 0.4$ , ${\bar{k}}_{2}^{P} = 0$ , $τ_{2} = 0.1536$

Inclusion properties (engineering constants):


$E_{1}$	240GPa
$E_{2}$	15GPa
$E_{3}$	15GPa
$ν_{12}$	0.2
$ν_{13}$	0.2
$ν_{23}$	0.07
$G_{12}$	27GPa
$G_{13}$	27GPa
$G_{23}$	7GPa
$v_{f}$	0.1
$a_{r}$	20.0

The inclusion shape is prolate, and the directions are aligned.

Results and discussion

Transient static responses of the composites predicted by mean-field homogenization are validated by comparing the responses to the prediction of FE-RVEs with the same microstructures.

The macroscale response of Composite 1 under uniaxial tension is plotted in Figure 14. The Mori-Tanaka homogenization method is used. The results compare well with the FE-RVE prediction.

The macroscale responses of Composite 2 under uniaxial tension in both the axial and transverse directions are plotted in Figure 15. The Mori-Tanaka homogenization method is used. The results compare well with the FE-RVE prediction.

Input files

multscale-prolate-vf10-visc.inp: One-element uniaxial tension test using Composite 1. Load is applied in the axial direction of the inclusion. Mori-Tanaka homogenization is used.
rve-prolate-vf10-visc.inp: FE-RVE model of Composite 1 under uniaxial tension loading. Load is applied in the axial direction of the inclusion.
multscale-prolate-vf10-visc-EC.inp: One-element uniaxial tension test using Composite 2. Load is applied in the axial direction of the inclusion. Mori-Tanaka homogenization is used.
rve-prolate-vf10-visc-EC.inp: FE-RVE model of Composite 2 under uniaxial tension loading. Load is applied in the axial direction of the inclusion.
multscale-prolate-vf10-visc-EC-transverse.inp: One-element uniaxial tension test using Composite 2. Load is applied in the transverse direction of the inclusion. Mori-Tanaka homogenization is used.
rve-prolate-vf10-visc-EC-transverse.inp: FE-RVE model of Composite 2 under uniaxial tension loading. Load is applied in the transverse direction of the inclusion.

Figures

Nonlinear composites

Elements tested

C3D8R

Features tested

Nonlinear multiscale materials modeled with mean-field homogenization methods.

Problem description

The verification tests consist of a set of single-element tests that use C3D8R elements under uniaxial tension or simple shear loading conditions. For constituents with plasticity, power law hardening is used,

\bar{σ} = σ_{Y} + k {({\bar{ϵ}}^{p l})}^{n},

where

\bar{σ}

is the yield stress and

{\bar{ϵ}}^{p l}

is the equivalent plastic strain. For plasticity models with rate dependency, the rate-dependent yield behavior is defined by the Cowper-Symonds overstress power law, which has the form

{\dot{\bar{ϵ}}}^{p l} = D {(\frac{\bar{σ}}{σ^{0}} - 1)}^{m},

where

σ^{0} = σ^{0} ({\bar{ϵ}}^{p l})

is the static stress-strain behavior.

Material:

Composite 1

Matrix properties:


$E$	75 GPa
$ν$	0.3
$σ_{Y}$	75 MPa
$k$	416 MPa
$n$	0.3895

Inclusion properties:


$E$	400 GPa
$ν$	0.2
$v_{f}$	0.1
$a_{r}$	1.0

The inclusions are spherical.

Composite 2

Matrix properties:


$E$	72.5 GPa
$ν$	0.34
$σ_{Y}$	250 MPa
$k$	173 MPa
$n$	0.46

Inclusion properties:


$E$	455 GPa
$ν$	0.15
$v_{f}$	0.2
$a_{r}$	10.0

The inclusion shape is prolate, and the orientations are randomly distributed in 3D.

Composite 3

Matrix properties:


$E$	100 GPa
$ν$	0.3
$σ_{Y}$	100 MPa
$k$	5 GPa
$n$	1.0
$D$	$0.3 \times 10^{- 3} s^{- 1}$
$m$	1.0

Inclusion properties:


$E$	500 GPa
$ν$	0.3
$σ_{Y}$	500 MPa
$k$	10 GPa
$n$	0.8
$D$	$0.6 \times 10^{- 3} s^{- 1}$
$m$	2.5
$v_{f}$	0.1
$a_{r}$	1.0

The inclusions are spherical.

Results and discussion

Nonlinear macroscale properties predicted by mean-field homogenization are validated.

The macroscale response of Composite 1 under uniaxial tension and simple shear loading is plotted in Figure 16 and Figure 17. The Mori-Tanaka homogenization method is used. The results compare well with the FE-RVE prediction. The results from both the uniaxial tension and the simple shear tests show that the isotropization methods have little influence on the prediction for this type of composite.

The macroscale response of Composite 2 under uniaxial tension loading is plotted in Figure 18. The Mori-Tanaka method is used for homogenization. 10 × 10 angle subdivisions are used to compute the numerical integration over orientation angles. The results are compared with those presented by Doghri (2006).

The macroscale response of Composite 3 under uniaxial tension loading is plotted in Figure 19. The Mori-Tanaka homogenization method is used. The results compare well with the FE-RVE prediction.

Input files

multscale-sphere-vf10-eiso.inp: One-element uniaxial tension test using Composite 1. Mori-Tanaka homogenization is used. The general method is used for isotropization, and the isotropized matrix modulus is applied only to the Eshelby tensor calculation.
multscale-sphere-vf10-piso.inp: One-element uniaxial tension test using Composite 1. Mori-Tanaka homogenization is used. The spectral method is used for isotropization, and the isotropized matrix modulus is applied to the calculation of Hill's tensor.
multscale-sphere-vf10-shear-eiso.inp: One-element simple shear test using Composite 1. Mori-Tanaka homogenization is used. The general method is used for isotropization, and the isotropized matrix modulus is applied only to the Eshelby tensor calculation.
multscale-sphere-vf10-shear-piso.inp: One-element simple shear test using Composite 1. Mori-Tanaka homogenization is used. The spectral method is used for isotropization, and the isotropized matrix modulus is applied to the calculation of Hill's tensor.
rve-sphere-vf10-elasplas.inp: FE-RVE model of Composite 1 under uniaxial tension loading.
rve-sphere-vf10-elasplas-shear.inp: FE-RVE model of Composite 1 under uniaxial tension loading.
multscale-prolate-random3d.inp: One-element uniaxial tension test using Composite 2.
multscale-sphere-visplas.inp: One-element uniaxial tension test using Composite 3.
rve-sphere-visplas.inp: FE-RVE model of Composite 3 under uniaxial tension loading.
power-uhard.f: User subroutine to define the power law hardening and power law rate dependency for Composite 3.

References

Doghri, I., and A. Ouaar, “Homogenization of Two-Phase Elasto-Plastic Composite Materials and Structures: Study of Tangent Operators, Cyclic Plasticity and Numerical Algorithms,” International Journal of Solids and Structures, vol. 40, pp. 1681–1712, 2003.
Doghri, I., and L. Tinel, “Micromechanics of Inelastic Composites with Misaligned Inclusions: Numerical Treatment of Orientation,” Computational Methods in Applied Mechanics and Engineering, vol. 195, pp. 1387–1406, 2006.
Pierard, O., and I. Doghri, “An Enhanced Affine Formulation and the Corresponding Numerical Algorithms for the Mean-Field Homogenization of Elasto-Viscoplastic Composites,” International Journal of Plasticity, vol. 22, pp. 131–157, 2006.

Figures